Confira aqui a resolução comentada da questão 138 (proporcionalidade) do caderno amarelo, matéria de MATEMÁTICA E SUAS TECNOLOGIAS.
Bom estudo!
Questão 138. Um clube deseja produzir miniaturas em escala do troféu que ganhou no último
campeonato. O troféu está representado na Figura 1 e é composto por uma base em formato
de um paralelepípedo reto-retângulo de madeira, sobre a qual estão fixadas três hastes
verticais que sustentam uma esfera de 30 cm de diâmetro, que fica centralizada sobre a base
de madeira. O troféu tem 100 cm de altura, incluída sua base.
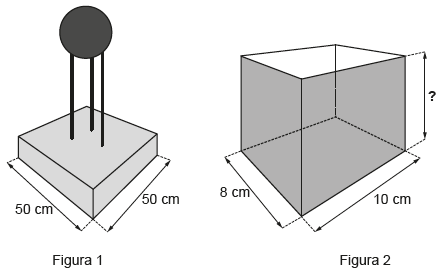
A miniatura desse troféu deverá ser instalada no interior de uma caixa de vidro, em formato de paralelepípedo reto-retângulo, cujas dimensões internas de sua base estão indicadas na Figura 2, de modo que a base do troféu seja colada na base da caixa e distante das paredes laterais da caixa de vidro em pelo menos 1 cm. Deve ainda haver uma distância de exatos 2 cm entre o topo da esfera e a tampa dessa caixa de vidro. Nessas condições deseja-se fazer a maior miniatura possível. A medida da altura, em centímetro, dessa caixa de vidro deverá ser igual a
A) 12.
B) 14.
C) 16.
D) 18.
E) 20.
Resolução
Observe que a base da caixa de vidro possui medidas iguais a 8 cm x 10 cm, e que a miniatura deve estar distante das paredes laterais em pelo menos 1 cm, sendo que a miniatura deve ser a maior possível, nestas condições.
Considerando os 8 cm de base e a distância de 1 cm em cada lado, podemos concluir que a
base da miniatura deverá ter medidas iguais a 6 cm x 6 cm.
O troféu, cuja base mede 50×50, passaria a ter 6×6, ou seja, estaríamos utilizando a seguinte
escala:
6/50 = 3/25
Aplicando a escala 3/25 na altura do troféu (100 cm):
100 . 3/25 = 12 cm
A questão informa que deve haver uma distância de exatos 2 cm entre o topo da esfera e a
tampa da caixa de vidro:
12 + 2 = 14 cm
Resposta: B
