Confira aqui a resolução comentada da questão 152 (geometria plana) do caderno amarelo, matéria de MATEMÁTICA E SUAS TECNOLOGIAS.
Bom estudo!
Questão 152. O proprietário de um apartamento decidiu instalar porcelanato no piso da sala. Essa sala tem formato retangular com 3,2 m de largura e 3,6 m de comprimento. As peças do porcelanato têm formato de um quadrado com lado medindo 80 cm. Esse porcelanato é vendido em dois tipos de caixas, com os preços indicados a seguir.
• Caixas do tipo A: 4 unidades de piso, R$ 35,00;
• Caixas do tipo B: 3 unidades de piso, R$ 27,00.
Na instalação do porcelanato, as peças podem ser recortadas e devem ser assentadas sem espaçamento entre elas, aproveitando-se ao máximo os recortes feitos.
A compra que atende às necessidades do proprietário, proporciona a menor sobra de pisos e resulta no menor preço é
A) 5 caixas do tipo A.
B) 1 caixa do tipo A e 4 caixas do tipo B.
C) 3 caixas do tipo A e 2 caixas do tipo B.
D) 5 caixas do tipo A e 1 caixa do tipo B.
E) 6 caixas do tipo B.
Resolução
Considerando que as peças de porcelanato possuem 80 cm x 80 cm, e que a instalação ocorre sem espaçamento entre eles, temos:
– O lado da sala que mede 3,2 m de largura terá exatamente 4 peças, pois 4 x 0,80 cm = 3,2 cm.
– O lado da sala que mede 3,6 m de comprimento terá 4,5 peças, pois 4,5 x 0,80 cm = 3,6 cm.
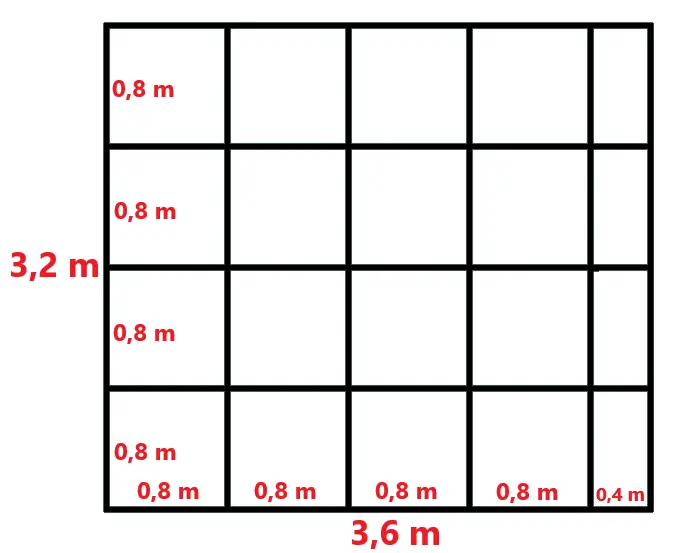
Com essas informações, podemos calcular a quantidade de peças necessárias para cobrir toda a sala, sem sobras:
4 x 4,5 = 18 peças
Analisando cada uma das alternativas:
A) 5 caixas do tipo A
Quantidade de pisos: 5 x 4 = 20
Valor: 5 x 35 = R$ 175,00
B) 1 caixa do tipo A e 4 caixas do tipo B.
Quantidade de pisos: 1×4 + 4×3 = 16
Valor: 1×35 + 4×27 = R$ 143,00
C) 3 caixas do tipo A e 2 caixas do tipo B.
Quantidade de pisos: 3×4 + 2×3 = 18
Valor: 3×35 + 2×27 = R$ 159,00
D) 5 caixas do tipo A e 1 caixa do tipo B.
Quantidade de pisos: 5×4 + 1×3 = 23
Valor: 5×35 + 1×27 = R$ 202,00
E) 6 caixas do tipo B.
Quantidade de pisos: 6 x 3 = 18
Valor: 6 x 27 = R$ 162,00
São necessários 18 pisos, ou seja, podemos descartar a alternativa B. Analisando as demais alternativas, a que resulta no menor preço é a letra C.
Resposta: C
