Confira aqui a resolução comentada da questão 154 (geometria plana) do caderno amarelo, matéria de MATEMÁTICA E SUAS TECNOLOGIAS.
Bom estudo!
Questão 154. O fenômeno das manifestações populares de massa traz à discussão como estimar o número de pessoas presentes nesse tipo de evento. Uma metodologia usada é: no momento do ápice do evento, é feita uma foto aérea da via pública principal na área ocupada, bem como das vias afluentes que apresentem aglomerações de pessoas que acessam a via principal. A foto é sobreposta por um mapa virtual das vias, ambos na mesma escala, fazendo-se um esboço geométrico da situação. Em seguida, subdivide-se o espaço total em trechos, quantificando a densidade, da seguinte forma:
• 4 pessoas por metro quadrado, se elas estiverem andando em uma mesma direção;
• 5 pessoas por metro quadrado, se elas estiverem se movimentando sem deixar o local;
• 6 pessoas por metro quadrado, se elas estiverem paradas.
É feito, então, o cálculo do total de pessoas, considerando os diversos trechos, e desconta-se daí 1 000 pessoas para cada carro de som fotografado.
Com essa metodologia, procederam-se aos cálculos para estimar o número de participantes na manifestação cujo esboço geométrico é dado na figura. Há três trechos na via principal: MN, NO e OP, e um trecho numa via afluente da principal: QR.
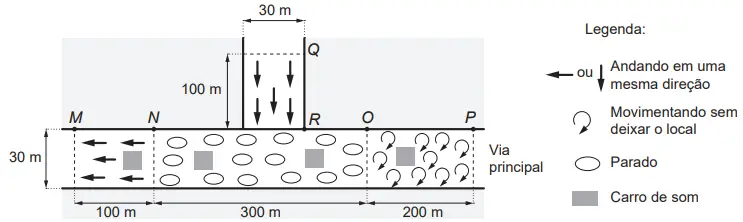
Segundo a metodologia descrita, o número estimado de pessoas presentes a essa manifestação foi igual a
A) 110 000.
B) 104 000.
C) 93 000.
D) 92 000.
E) 87 000.
Resolução
Analisaremos cada um dos trechos QR, MN, NO e OP:
- Trecho QR
Área: 30 x 100 = 3.000 m²
Como as pessoas estão andando em uma mesma direção, então são estimadas 4 pessoas por m²:
4 x 3.000 = 12.000 pessoas
- Trecho MN
Área: 30 x 100 = 3.000 m²
Como as pessoas estão andando em uma mesma direção, são estimadas 4 pessoas por m²:
4 x 3.000 = 12.000 pessoas
- Trecho NO
Área: 30 x 300 = 9.000 m²
Como as pessoas estão paradas, são estimadas 6 pessoas por m²:
6 x 9.000 = 54.000 pessoas
- Trecho OP
Área: 30 x 200 = 6.000 m²
Como as pessoas estão se movimentando sem deixar o local, são estimadas 5 pessoas por m²:
5 x 6.000 = 30.000 pessoas
Total:
12.000 + 12.000 + 54.000 + 30.000 = 108.000
Para finalizar, devemos descontar 1.000 pessoas por carro de som. Observando a figura, temos 4 carros de som.
4 x 1.000 = 4.000
Total após o desconto referente aos carros de som:
108.000 – 4.000 = 104.000
Resposta: B
