Confira aqui a resolução comentada da questão 176 (conjuntos) do caderno amarelo, matéria de MATEMÁTICA E SUAS TECNOLOGIAS.
Bom estudo!
Questão 176. Um grupo sanguíneo, ou tipo sanguíneo, baseia-se na presença ou ausência de dois antígenos, A e B, na superfície das células vermelhas do sangue. Como dois antígenos estão envolvidos, os quatro tipos sanguíneos distintos são:
• Tipo A: apenas o antígeno A está presente;
• Tipo B: apenas o antígeno B está presente;
• Tipo AB: ambos os antígenos estão presentes;
• Tipo O: nenhum dos antígenos está presente.
Foram coletadas amostras de sangue de 200 pessoas e, após análise laboratorial, foi identificado que em 100 amostras está presente o antígeno A, em 110 amostras há presença do antígeno B e em 20 amostras nenhum dos antígenos está presente.
Dessas pessoas que foram submetidas à coleta de sangue, o número das que possuem o tipo sanguíneo A é igual a
A) 30.
B) 60.
C) 70.
D) 90.
E) 100.
Considere:
x = quantidade de amostras com apenas o antígeno A (Tipo A)
y = quantidade de amostras com ambos os antígenos (Tipo AB)
z = quantidade de amostras com apenas o antígeno B (Tipo B)
Com essas informações, podemos desenhar o seguinte diagrama:
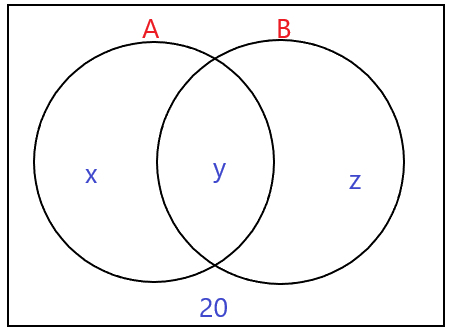
Como “foi identificado que em 100 amostras está presente o antígeno A”:
x + y = 100
x = 100 – y
Como “em 110 amostras há presença do antígeno B”:
y + z = 110
z = 110 – y
Como “foram coletadas amostras de sangue de 200 pessoas e, …, em 20 amostras nenhum dos antígenos está presente”.
x + y + z = 180
Substituindo as equações 1 e 2 na equação 3:
x + y + z = 180
(100 – y) + y + (110 – y) = 180
100 – y + y + 110 – y = 180
210 – y = 180
y = 210 – 180
y = 30
Calculando a quantidade de amostras que possuem o tipo sanguíneo A:
x = 100 – y
x = 100 – 30
x = 70
Resposta: C
