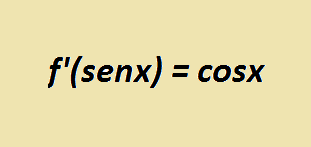Veja aqui qual é a derivada da função seno, onde apresentaremos uma demonstração detalhada, utilizando os conceitos de limites.
Não deixe de ver também nossas publicações sobre outros tópicos do Cálculo Diferencial.
Bom estudo!
A demonstração da função seno será feita utilizando a definição de derivada:
Temos:
O próximo passo será utilizar a fórmula do seno da soma em sen(x+h), a saber:
Aplicando a propriedade da soma dos limites:
Colocando sen(x) em evidência no segundo termo:
Multiplicando o numerador e o denominador do segundo limite por cos(h) + 1:
Simplificando:
Utilizando a relação fundamental da trigonometria sen²h + cos²h = 1, temos:
Pela propriedade da multiplicação de limites:
Como sen(h) / h = 1, temos:
Conclusão:
Gostou da demonstração da derivada da função seno?
Deixe o seu comentário.