Confira aqui tudo o que você precisa saber sobre as coordenadas do vértice de uma parábola, os chamados x e y do vértice.

Não deixe de ver também nossos outros conteúdos sobre as funções quadráticas, também conhecidas como funções do segundo grau.

Bom estudo!

 

 

As coordenadas do vértice de uma parábola podem ser calculadas através de duas fórmulas bem simples. Veremos abaixo quais são e como é feita a dedução dessas fórmulas.

Sabemos que uma função do segundo grau é do tipo:

f(x) = ax + bx + c, onde a≠0.

 

A forma mais simples de calcular as raízes da função quadrática é através da fórmula de Bhaskara:

 

Por ela, podemos observar que as duas raízes são:

 

Como uma parábola é simétrica em relação ao seu eixo, a coordenada x do vértice é exatamente a média aritmética de x’ e x”.

 

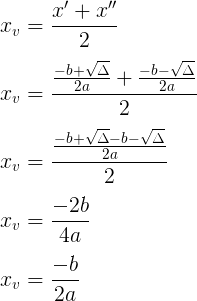
Daí, a fórmula utilizada para calcular o x do vértice de uma parábola é:

 

 

Agora que já sabemos o valor do x do vértice, podemos calcular o y do vértice. Para tanto, basta substituirmos o valor conhecido na função f.

 

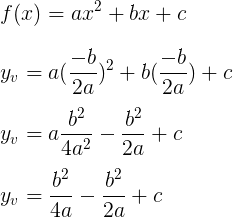
Tirando o MMC da segunda parte da igualdade:

 

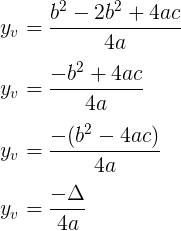
Daí, a fórmula utilizada para calcular o y do vértice é:

 

 

Concluindo, as coordenadas do vértice de uma parábola são:

 

 

Exemplo. Calcular as coordenadas do vértice da parábola atrelada a função f(x) = x² + 4x – 3.

 

Temos que:

a = 1

b = 4

c = -3

 

Calculando o valor de Δ:

Δ = b² – 4ac = 4² – 4.1.(-3) = 16 + 12 = 28

 

Calculando o x do vértice:

x_v = -b/2a = -4/2.1 = -2

 

Calculando o y do vértice:

y_v = -Δ/4a = -28/4.1 = -7

 

Daí, as coordenadas do vértice da parábola são (-2, -7).

 

 

Aprendeu a deduzir as fórmulas do x e y do vértice da parábola?

Deixe o seu comentário.