Estudando matemática para concursos? Confira aqui as posições relativas entre ponto e circunferência, onde você aprenderá também a calcular a distância entre ambos.

Não deixe de ver também nossos conteúdos sobre os demais tópicos da geometria analítica.

Bom estudo!

 

 

Analisando as posições relativas entre um ponto e uma circunferência, temos três casos possíveis:

• O ponto pode pertencer à circunferência.
• O ponto pode ser externo à circunferência.
• O ponto pode ser interno à circunferência.

Vamos analisar cada um dos casos.

 

 

QUANDO O PONTO PERTENCE À CIRCUNFERÊNCIA

Analisando a figura, é possível observar que a distância entre o ponto P e o centro C é igual ao raio.

d_PC = r ⇒ P pertence à circunferência

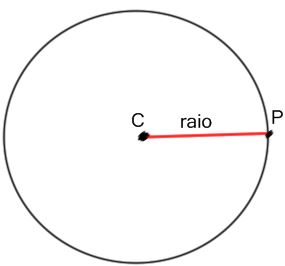Neste caso não existe nenhum cálculo a ser feito. A distância entre o ponto P e a circunferência é zero.

 

 

QUANDO O PONTO É EXTERNO À CIRCUNFERÊNCIA

Veja na figura que a distância entre o ponto P e o centro C é maior que o raio.

d_PC > r ⇒ P é externo à circunferência

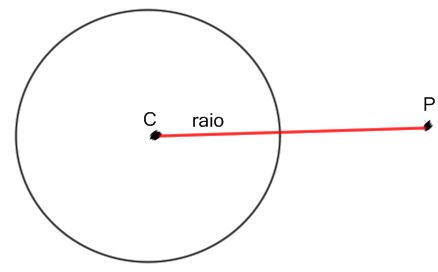A distância entre o ponto P e a circunferência é a distância entre o ponto P e o centro C, subtraída pelo raio da circunferência. Devemos então calcular a distância entre os pontos P e C, e subtrair a medida do raio.

 

Exemplo. Calcular a distância entre o ponto P(10, 5) e a circunferência (x – 3)² + (y – 4)² = 25.

A equação reduzida da circunferência nos fornece as seguintes informações:

– o raio é igual a 5

– o centro é C(3, 4)

 

O primeiro passo é calcular a distância entre os pontos P(10, 5) e C(3, 4).

d² = (10 – 3)² + (5 – 4)²

d² = 7² + 1²

d² = 49 + 1

d² = 50

d = √50

d = 5√2

 

Como 5√2 > 5, podemos afirmar que o ponto é exterior à circunferência e que a distância entre eles mede 5√2 – 5.

 

 

QUANDO O PONTO É INTERNO À CIRCUNFERÊNCIA

Neste caso, a distância entre o ponto P e o centro C é menor do que o raio da circunferência.

d_PC < r ⇒ P é interno à circunferência

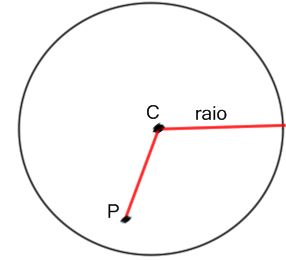A distância entre o ponto P e a circunferência é a medida do raio, subtraída pela medida entre o ponto P e o centro C da circunferência. Devemos então calcular a distância entre os pontos P e C, e efetuarmos a subtração do raio pela distância entre P e C.

 

Exemplo. Calcular a distância entre o ponto P (3, 4) e a circunferência (x – 2)² + (y – 3)² = 25.

A equação reduzida nos informa que

– o raio é igual a 5

– o centro é C(2, 3)

 

Calculando a distância entre os pontos P e C:

d² = (3 – 2)² + (4 – 3)²

d² = 1² + 1²

d² = 1 + 1

d² = 2

d = √2

 

Como √2 < 5, podemos concluir que o ponto é interno à circunferência e a distância entre eles mede 5 – √2.

 

 

Gostou do nosso post sobre a posição relativa entre ponto e circunferência, e sobre como é feito o cálculo da distância entre eles?

Deixe o seu comentário.