A área do cone reto pode ser calculada através de uma fórmula matemática bem simples. Nesta página veremos a dedução e alguns exemplos de utilização.
Não deixe de ver também os nossos outros conteúdos sobre geometria espacial.
Bom estudo!
Antes de aprendermos a fórmula matemática utilizada para calcular a área do cone reto, vamos relembrar a definição deste objeto tridimensional.
Um cone é um sólido geométrico que possui uma base no formato de uma circunferência e um vértice fora do plano que contém a base. Em especial, um cone reto é aquele onde a reta que passa pelo vértice e pelo centro da base é perpendicular ao plano que contém a base. Veja:
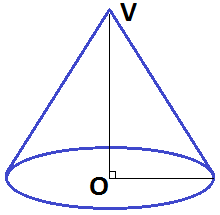
Para calcularmos a área do cone, vamos realizar a planificação das superfícies. Veja:
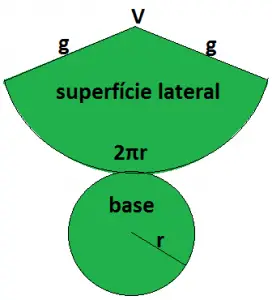
Nota-se que a área total do cone é a soma da área da base com a área lateral.
At = Ab + Al
Vamos calcular calcular cada uma dessas áreas.
Área da base (Ab)
A área da base do cone é a área do círculo de raio r.
Ab = π.r²
Área lateral (Al)
A área lateral é a área do setor circular cujo raio é a geratriz (g) do cone e cujo comprimento do arco é igual a 2πr (perímetro da base).
Podemos obter a área do setor circular através da regra de três:

Daí,
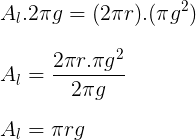
Área total do cone reto (At)
Como dito, a área total de um cone reto é a soma da área da base com a área lateral. Temos:
At = Ab + Al
At = π.r² + π.r.g
At = π.r.(g + r)
Pelos cálculos acima, a fórmula matemática utilizada para calcular a área de um cone reto é dada por:
At = π.r.(g + r)
