Após vários pedidos dos nossos fiéis estudantes, hoje falaremos sobre o algoritmo da divisão, onde abordaremos especificamente os números inteiros e positivos.

O conteúdo não é complicado, porém muita gente se confunde na hora da prova, principalmente devido ao uso excessivo de calculadoras.

Bom estudo!

DIVISÃO

A divisão faz parte do grupo de 4 operações básicas da matemática, e talvez seja a mais difícil delas. Está ligada a ideia de repartir certas quantidades em partes iguais.

Exemplo:

Paulinho dividiu as 12 uvas que tinha com seus dois irmãos, de modo que cada um deles ficou com a mesma quantidade. É fácil verificar que cada um deles ficou com 4 uvas.

Podemos simbolizar a divisão de três formas distintas: utilizando dois pontos (:), utilizando um traço com dois pontos (÷) ou utilizando uma barra (/). Veja:

12 : 3 = 4

12 ÷ 3 = 4

12 / 3 = 4

Neste exemplo, 12 é o dividendo, 3 é o divisor, e 4 é o quociente.

DIVIDENDO ÷ DIVISOR = QUOCIENTE

Observação:

• Não existe divisão pelo zero, ou seja, o divisor deve ser diferente de zero.

O RESTO

O que aconteceria em nosso exemplo se Paulinho tivesse 13 uvas ao invés de 12?

A 13ª uva sobraria. Essa uva é chamada de resto na multiplicação.

Dizemos que 13 dividido por 3 é igual a 4, com resto 1.

Observações:

• O resto é sempre menor que o divisor;
• Se o resto é igual a zero, a divisão é exata.

O ALGORITMO

A estrutura do algoritmo da divisão é a seguinte:

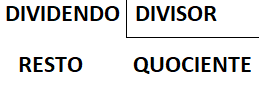
Para utilizarmos o algoritmo, o dividendo e o divisor devem ser posicionados conforme a figura acima. Ao contrário da multiplicação, a divisão é efetuada da esquerda para a direita.

Vejamos alguns exemplos de como calcular o resto e o quociente.

Exemplo 1. Dividir 125 por 5.

O primeiro passo é montar o algoritmo.

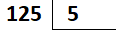
Como informado, a divisão é feita da esquerda para a direita.

A primeira pergunta que fazemos é:

• 1 é maior que 5?

Não. Como a resposta foi não, faremos a mesma pergunta para o 12:

• 12 é maior que 5?

Sim. 12 dividido por 5 é igual a 2, com resto também igual a 2.

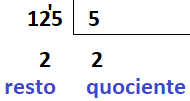
Como ainda temos um algarismo após o 12, este será “baixado” da seguinte forma:

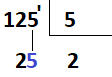
Nosso próximo passo é dividir o 25 pelo divisor 5.

Temos que 25 dividido por 5 é igual a 5, com resto zero.

Neste caso, acrescentamos o 5 após o 2 no quociente, e o resto zero abaixo do 25.

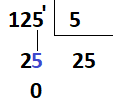
Conclusão: 125 dividido por 5 é igual a 25, com resto igual a zero.

Exemplo 2. Dividir 4562 por 3.

Montando o algoritmo:

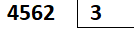
4 é maior que 3?

Sim. 4 dividido por 3 é igual a 1, com resto 1.

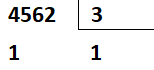
“Baixando” o 5, temos que 15 dividido por 3 é igual a 5, que será acrescentado após o 1 do quociente.

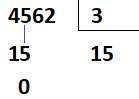
“Baixando” o 6, temos que 6 dividido por 3 é igual a 2, que será acrescentado após o 5 do quociente.

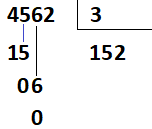
“Baixando” o 2, temos que 2 é menor que 3. Neste caso, acrescentamos um zero ao quociente, e consideramos que o resto é igual a 2.

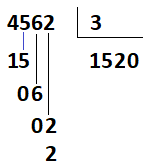
Conclusão: 4562 dividido por 3 é igual a 1520, com resto 2.

Exemplo 3. Dividir 4620 por 21.

Veja abaixo que não importa a quantidade de algarismos do divisor, o procedimento será sempre o mesmo.

Neste exemplo temos um caso especial. Sempre que o resto for igual a zero, e existir outro zero para “baixar”, acrescentaremos um zero no quociente. Veja:

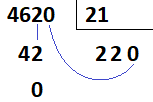
• 4 é menor que 21
• 46 dividido por 21 é igual a 2, com resto 4
• baixando o 2, 42 dividido por 21 é igual a 2, com resto 2
• como só existe um zero para ser baixado, este será acrescentado no quociente

Conclusão: 4620 dividido por 21 é igual a 220.

Aprendeu a efetuar a divisão com o auxílio do algoritmo?

Deixe o seu comentário.