Estudando matemática para concursos? Confira aqui vários exercícios resolvidos sobre a elipse, todos retirados dos últimos concursos públicos.
Não deixe de ver também nossos exercícios resolvidos sobre os outros tópicos da geometria analítica.
Bom estudo!
Questão 1 (IFB – 2017). Considerando uma elipse com centro na origem, focos num dos eixos coordenados e passando pelos pontos (5, 0) e (0, 13), determine os focos da elipse.
a) (13, 0) e (– 13, 0)
b) (0, 13) e (0, – 13)
c) (12, 0) e (– 12, 0)
d) (0, 12) e (0, – 12)
e) (5, 0) e (– 5, 0)
Resolução
Como sabemos, em toda elipse vale a relação a² = b² + c², onde 2a é a distância do eixo maior, 2b é a distância do eixo menor e 2c é a distância entre os focos.
Pelas informações fornecidas pelo enunciado, temos que a = 13 e b = 5. Veja no desenho abaixo:
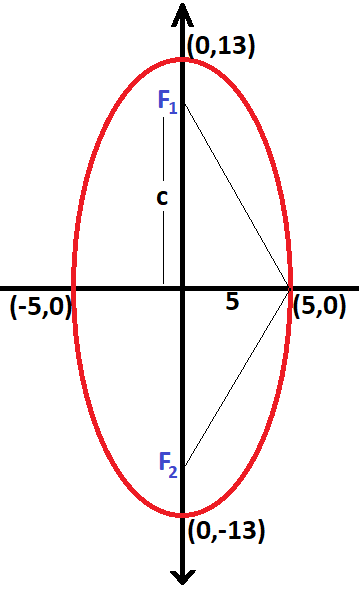
a² = b² + c²
13² = 5² + c²
169 = 25 + c²
c² = 169 – 25
c² = 144
c = 12
Como c = 12, os focos da elipse são (0,12) e (0,-12).
Resposta: D
Questão 2 (ESPCEX 2013) Sobre a curva 9x² + 25y² − 36x + 50y − 164 = 0, assinale a alternativa correta.
a) Seu centro é (−2,1).
b) A medida do seu eixo maior é 25.
c) A medida do seu eixo menor é 9.
d) A distância focal é 4.
e) Sua excentricidade é 0,8.
Resolução
Nosso primeiro passo é descobrir se a equação realmente representa uma elipse. Nossa estratégia será completar os quadrados.
9x² + 25y² − 36x + 50y − 164 = 0
9x² – 36x + 36 – 36 + 25y² + 50y + 25 – 25 − 164 = 0
(3x – 6)² + (5y + 5)² – 225 = 0
(3x – 6)² + (5y + 5)² = 225
9.(x – 2)² + 25.(y + 1)² = 225
Dividindo ambos os lados da equação por 225:
![]()
Daí, podemos concluir que trata-se de uma elipse de centro (2, -1), com a=5 e b=3.
Eixo maior = 2a = 10
Eixo menor = 2b = 6
Podemos calcular o valor de c através da seguinte relação:
a² = b² + c²
5² = 3² + c²
25 = 9 + c²
c² = 25 – 9
c² = 16
c = √16
c = 4
Distância focal = 2c = 8
Calculando a excentricidade:
c/a = 4/5 = 0,8
Resposta: E
Gostou dos nossos exercícios resolvidos sobre a elipse?
Deixe o seu comentário.
