Procurando exercícios resolvidos sobre as combinações? Chegou ao site certo. Todas as questões apresentadas a seguir foram aplicadas em provas de concursos públicos.
Antes de acompanhar os exercícios, pede-se que o aluno tenha conhecimentos sobre os diversos assuntos de análise combinatória.
Bom estudo!
Questão 1 (PC PARÁ – FUNCAB 2016). Durante uma operação policial, 15 homens foram detidos e transportados para a delegacia em três transportes, o primeiro com seis lugares, o segundo com cinco lugares e o terceiro com quatro lugares. O número de maneiras, que os detidos podem ser transportados para delegacia, é:
a) C15,6 . C15,5 . C15,4
b) P6 . P5 . P4
c) A15,6 . A15,5 . A15,4
d) (P15) : (P6 + P5 + P4)
e) C15,6 . C9,5 . C4,4
Resolução
O primeiro ponto a ser analisado é se a questão deixou claro se o local onde cada preso se sentou no carro é relevante ou não.
Teremos uma combinação caso a posição de cada preso não seja importante para a questão. Da mesma forma, caso a posição dentro do carro seja relevante, teremos um arranjo.
No meu entendimento, quando a questão pergunta de quantas maneiras os detidos podem ser transportados, devemos considerar sim a posição dentro do carro.
Resolvendo…
No carro com 6 lugares, sabendo que temos 15 presos, a quantidade de opções será a combinação C15,6.
No carro com 5 lugares, sabendo que 6 já estão no carro anterior, a quantidade de opções será a combinação C9,5.
No carro com 4 lugares, sabendo que 11 presos já estão nos outros carros, a quantidade de opções será a combinação C4,4.
A quantidade total de opções será:
C15,6 . C9,5 . C4,4
Perceba que a ordem dos carros não importa, o resultado final será sempre o mesmo.
Resposta: E
Questão 2 (PM PE – UPENET 2016). Um grupo de inquérito é formado por 8 oficiais e 4 soldados. Para analisar os processos, formam-se comissões com 4 oficiais e 2 soldados. Sendo A um oficial qualquer e B um soldado qualquer, qual é o número de comissões de que participa o oficial A e não participa o soldado B?
A) 105
B) 87
C) 64
D) 256
E) 504
Resolução
Para formarmos um grupo de 4 oficiais, onde o oficial A precisa estar, precisamos escolher os outros 3 entre 7 oficiais restantes. Temos uma combinação de 3 em 7:
C3,7 = 7!/3!.4! = 35
Para formarmos um par de 2 soldados, onde o soldado B não pode estar, precisamos escolher os 2 entre os outros 3 soldados restantes. Temos uma combinação de 2 em 3:
C2,3 = 3!/2!.1! = 3
O total será:
35 x 3 = 105
Resposta: A
Questão 3 (PM MA – FGV 2012). Lucas é vigia noturno de uma empresa e deve escolher os três dias em que trabalhará na próxima semana. Para fazer isso ele deve preencher uma ficha como a apresentada a seguir.
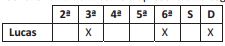
O número de maneiras diferentes que Lucas pode preencher essa ficha é:
(A) 35.
(B) 70.
(C) 105.
(D) 210.
(E) 343.
Resolução
Lucas deve escolher 3 em 7 dias.
Trata-se de uma combinação simples de 3 em 7:
C(3,7) = 7! / 3!.4! = 7.6.5/3.2.1 = 35
Resposta: A
Questão 4 (BANESTES – IDECAN 2012). Numa determinada agência bancária estão disponíveis 12 caixas eletrônicos. De quantas maneiras é possível escolher 3 desses caixas para se efetuar um serviço de manutenção?
(A) 150
(B) 172
(C) 180
(D) 220
(E) 240
Resolução
A questão busca escolher 3 caixas entre 12. Se quisermos calcular a quantidade, basta verificarmos a combinação de 3 em 12:
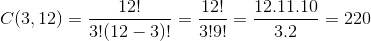
Resposta: D
Questão 5 (BOMBEIROS MG – IGETEC 2008). Sejam s e t retas paralelas. Os pontos A,B,C e D pertencem a s e, E,F,G e H são pontos da reta t . Quantos triângulos distintos podemos formar, tendo como vértices os pontos A,B,C, D,E,F,G e H ?
a) 24
b) 42
c) 56
d) 48
Resolução
Reta s: ——-A——B——C——D——
Reta t: ——-E——F——G——H——
Vamos considerar dois casos:
1) Um vértice está na reta s e dois vértices na reta t:
Na reta s temos 4 opções e na reta t a quantidade de combinações C(2,4) = 6. Total de 4×6 = 24 triângulos
2) Um vértice está na reta t e dois vértices na reta s:
Na reta t temos 4 opções e na reta s a quantidade de combinações C(2,4) = 6. Total de 4×6 = 24 triângulos
Total de 48 triângulos
Resposta: D
Questão 6 (BB – CESGRANRIO 2010). Uma artesã de bijuterias fabrica um colar de contas no qual utiliza 16 contas pequenas e duas contas grandes, cujo modelo é apresentado abaixo.
Os critérios que ela utiliza para montar cada colar são os seguintes:
• as contas pequenas são todas da mesma cor;
• contas grandes devem ter cores diferentes;
• se as contas pequenas forem da cor “x”, nenhuma conta grande pode ser da cor “x”.
Sabendo-se que a artesã dispõe de contas pequenas brancas, pretas, azuis e laranjas e de contas grandes brancas,
vermelhas, verdes, azuis e rosas, de quantos modos distintos ela pode escolher as cores das contas que irão compor
um colar?
(A) 28
(B) 30
(C) 32
(D) 40
(E) 42
Resolução
Cores para as contas pequenas: branca, preta, azul e laranja
Cores para as contas grandes: branca, vermelha, verde, azul e rosa
Se escolhermos branca ou azul para as contas pequenas, cores comuns as duas, para escolhermos as cores das contas grandes teremos uma combinação de 2 em 4, logo:
2 x C(2,4) = 2 x 6 = 12
Se escolhermos preta ou laranja para as contas pequenas, cores que não podem ser usadas nas contas grandes, para escolhermos as cores das contas grandes teremos uma combinação de 2 em 5, logo:
2 x C(2,5) = 2 x 10 = 20
Total: 12 + 20 = 32
Resposta: C
Questão 7 (PM PE – IAUPE). Para formar uma comissão com quatro policiais militares, estarão à disposição cinco oficiais e quatro praças. Quantas comissões distintas poderão ser formadas, de maneira que, em cada uma delas, haja, pelo menos, um oficial?
a) 225
b) 20
c) 60
d) 125
e) 120
Resolução
Temos 9 policiais, sendo 5 oficiais e 4 praças. Calcularemos a quantidade total de comissões e subtrairemos pela quantidade de comissões sem oficiais.
Calculando a quantidade total de comissões possíveis:
C9,4 = 9!/4!(9-4)!
C9,4 = 9!/4!5!
C9,4 = 9.8.7.6/4.3.2
C9,4 = 126
Calculando a quantidade de comissões possíveis sem nenhum oficial:
C4,4 = 1
Total: 126 – 1 = 125
Resposta: D
Gostou dos nossos exercícios resolvidos sobre combinação?
Deixe o seu comentário.
