Confira aqui vários exercícios resolvidos sobre o setor circular. Lembrando que todas as questões são de provas de concursos.
O ideal é que o aluno leia o nosso conteúdo sobre o assunto na sessão “material didático” e que também tenha conhecimentos sobre área do círculo e regra de três.
Bom estudo!
Questão 1 (Pref. Mun. do RJ – 2016). Admita que de uma pizza circular de centro C e raio R cortam-se n fatias congruentes e todas com a forma de setores circulares de raio R e centro C. Se cada um desses setores tem ângulo central medindo 0,5 radiano, o maior valor de n é igual a:
a) 12
b) 8
c) 6
d) 4
Resolução
A questão deseja saber a quantidade de setores circulares que pode ser obtida de uma circunferência, considerando que estes devem ter ângulo central igual a 0,5 radiano (0,5π).
Sabemos que uma circunferência possui arco total de 2 radianos (2π), assim, para calcularmos a quantidade de setores, basta efetuarmos a seguinte divisão:
2π / 0,5π = 4
Veja como fica na figura:
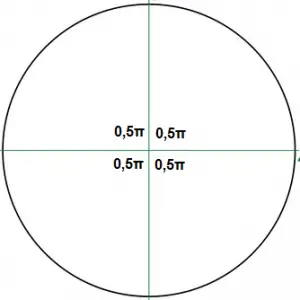
Resposta: D
Questão 2 (Metrô SP – FCC 2015). A partir do centro de uma torta circular retira-se uma fatia (setor circular) que corresponde à 35% do total da torta. A fatia retirada é um setor circular de ângulo central igual a
a) 70°
b) 63°
c) 145°
d) 234°
e) 126°
Resolução
Como sabemos, a área de um setor circular é diretamente proporcional à medida do ângulo central, assim, dizer que o setor circular retirado corresponde a 35% da torta, é a mesma coisa que dizer que a área do setor circular corresponde a 35% da área do círculo, de onde podemos concluir que o ângulo central é 35% de 360º.
360 . 0,35 = 126°
Resposta: E
Questão 3 (Marilândia ES – IDECAN 2016). Uma pista de corrida foi construída com o formato de um setor circular, conforme apresentado a seguir.
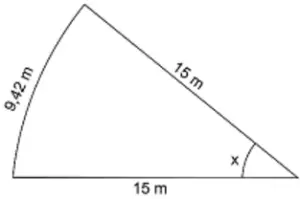
Pode‐se afirmar que o valor do ângulo x é igual a
(Considere: π = 3,14.)
a) 30°.
b) 36°.
c) 42°.
d) 45°.
Resolução
Sabemos o comprimento do arco (9,42 m).
Vamos utilizar regra de três trabalhando com radianos:
360 ————— x
2πr —————- 9,42
360.9,42 = 2πrx
3391,2 = 2.3,14.15.x
3391,2 = 94,2.x
x = 3391,2 / 94,2
x = 36º
Resposta: B
