Nesta página iremos aprender a calcular a área de uma coroa circular, nome dado a região limitada por dois círculos cujos centros são coincidentes, ou seja, concêntricos.
Não se trata de um conteúdo constantemente cobrado em concursos públicos, sendo exigido com mais frequência em concursos onde pede-se muito geometria plana.
Bom estudo!
Sejam duas circunferências C1 e C2, concêntricas, cujos raios medem r e R, respectivamente. Veja a figura:
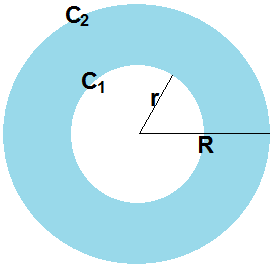
Observe que a área da coroa circular de cor azul e delimitada pelas circunferências C1 e C2 é exatamente a diferença entre as áreas dos círculos de raios R e r.
A1 = π.r²
A2 = π.R²
Logo, a área da coroa circular é igual a:
A = A2 – A1 = π.R² – π.r²
Exemplo 1: Calcular a área da coroa circular representada na figura abaixo.
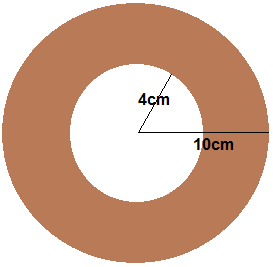
Área do círculo menor:
A1 = π.r² = π.4² = 16π
Área do círculo maior:
A2 = π.R² = π.10² = 100π
Área da coroa circular:
A = A2 – A1
A = 100π – 16π
A = 84π
Exemplo 2: Calcular a área da coroa circular representada na figura.
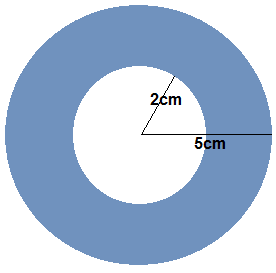
Área do círculo menor:
A1 = π.r² = π.2² = 4π
Área do círculo maior:
A2 = π.R² = π.5² = 25π
Área da coroa circular:
A = A2 – A1
A = 25π – 4π
A = 21π
