MULTIPLICAÇÃO DE MATRIZES

Olá amigos internautas. Vamos aprender nesta página a identificar quando é possível e como é definida a multiplicação de matrizes.

O ideal é que o estudante já tenha lido o nosso conteúdo sobre a definição e as propriedades das matrizes.

Bom estudo!

 

 

INTRODUÇÃO

Quando representamos matrizes, a característica mais importante que deve ser informada é a quantidade de linhas e colunas. Por isso que a representação de uma matriz A qualquer é feita por A_mxn, onde m é a quantidade de linhas e n é a quantidade de colunas da matriz A.

Podemos ainda representar um elemento qualquer desta matriz por a_ij, onde 1≤i≤m e 1≤j≤n.

Por exemplo, a matriz representada por A_5×4 possui 5 linhas e 4 colunas, e o elemento localizado na segunda linha e na terceira coluna é o a₂₃.

 

 

QUANDO PODEMOS MULTIPLICAR MATRIZES

A multiplicação não é definida para todo par de matrizes. Existe uma regra bem simples que deve ser observada para que seja possível essa multiplicação. Veja:

A multiplicação de duas matrizes A e B somente é possível quando o número de colunas da primeira (A) é igual ao número de linhas da segunda (B) matriz. O resultado dessa multiplicação será uma matriz C, cujo número de linhas é igual ao número de linhas da primeira e o número de colunas é igual ao número de colunas da segunda.

Observe o esquema abaixo para facilitar o entendimento:

Uma coisa importante a ser observada é que o fato de A.B ser possível não faz com que a multiplicação B.A também seja. Devemos analisar da mesma forma a quantidade de linhas e colunas. Em nosso esquema acima, B.A somente será possível se p = m.

 

Exemplo 1

A multiplicação das matrizes abaixo é possível pois a quantidade de colunas da matriz A é igual a quantidade de linhas da matriz B. Temos ainda que o resultado será uma matriz C com a quantidade de linhas de A e a quantidade de colunas de B.

 

Exemplo 2

A multiplicação das matrizes abaixo não é possível pois a quantidade de colunas da matriz A é diferente da quantidade de linhas da matriz B.

 

 

COMO É FEITA A MULTIPLICAÇÃO DE MATRIZES

Dadas duas matrizes A = (a_ij)_mxp e B = (b_ij)_pxn, o produto A.B é a matriz C = (c_ij)_mxn, onde cada elemento c_ij é obtido por meio da soma dos produtos dos elementos correspondentes da i-ésima linha da matriz A pelos elementos da j-ésima coluna da matriz B.

Achou complicado? Vamos fazer um exemplo para mostrarmos que é mais fácil do que parece.

 

Exemplo 3

Sejam as matrizes A_(3×3) e B_(3×2) abaixo. O produto A.B é possível pois o número de colunas da matriz A é igual ao número de linhas da matriz B.

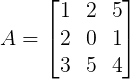
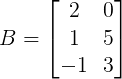
Como vimos, cada elemento da matriz C = A.B será obtido pela soma dos produtos dos elementos correspondentes da linha de A pela coluna de B.

 

Calculando o elemento c₁₁:

c₁₁ = a₁₁.b₁₁ + a₁₂.b₂₁: + a₁₃.b₃₁

c₁₁ = 1.2 + 2.1 + 5.(-1)

c₁₁ = 2 + 2 – 5

c₁₁ = -1

 

Calculando o elemento c₁₂:

c₁₂ = a₁₁.b₁₂ + a₁₂.b₂₂: + a₁₃.b₃₂

c₁₂ = 1.0 + 2.5 + 5.3

c₁₂ = 0 + 10 + 15

c₁₂ = 25

 

Calculando o elemento c₂₁:

c₂₁ = a₂₁.b₁₁ + a₂₂.b₂₁: + a₂₃.b₃₁

c₂₁ = 2.2 + 0.1 + 1.(-1)

c₂₁ = 4 + 0 – 1

c₂₁ = 3

 

Calculando o elemento c₂₂:

c₂₂ = a₂₁.b₁₂ + a₂₂.b₂₂: + a₂₃.b₃₂

c₂₂ = 2.0 + 0.5 + 1.3

c₂₂ = 0 + 0 + 3

c₂₂ = 3

 

Calculando o elemento c₃₁:

c₃₁ = a₃₁.b₁₁ + a₃₂.b₂₁: + a₃₃.b₃₁

c₃₁ = 3.2 + 5.1 + 4.(-1)

c₃₁ = 6 + 5 – 4

c₃₁ = 7

 

Calculando o elemento c₃₂:

c₃₂ = a₃₁.b₁₂ + a₃₂.b₂₂: + a₃₃.b₃₂

c₃₂ = 3.0 + 5.5 + 4.3

c₃₂ = 0 + 25 + 12

c₃₂ = 37

 

O produto das matrizes A_(3×3) e B_(3×2) será uma matriz C_(3×2), a saber:

 

 

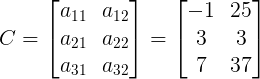
PROPRIEDADES

Agora que já sabemos como multiplicar matrizes, é importante sabermos também as propriedades da multiplicação:

a) associativa: (A.B) . C = A . (B.C)

b) distributiva em relação à adição: A . (B+C) = A.B + A.C

c) elemento neutro: A . I_n = I_n . A = A, sendo I_n a matriz identidade de ordem n

Obs: A propriedade comutativa, exceto por algumas coincidências, não vale para a multiplicação de matrizes, ou seja, A.B ≠ B.A