Procurando exercícios resolvidos sobre o volume de um cilindro? Confira aqui várias questões comentadas, todas retiradas dos últimos concursos.
Não deixe de ver também nossos exercícios resolvidos sobre os outros conteúdos de geometria espacial.
Bom estudo!
Questão 1 (PM ES – Funcab 2013). Supondo as dimensões internas de cada pino plástico utilizado na embalagem de cocaína como sendo um cilindro de raio 0,5 cm e altura 4 cm, o valor do volume total de cocaína, desse pino plástico, completamente cheio, em cm³, será de:
(Adote o valor aproximado de π= 3 )
A) 2,5
B) 3
C) 3,5
D) 4
E) 4,5
Resolução
Vamos utilizar a fórmula matemática que calcula o volume de um cilindro.
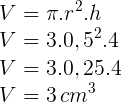
Resposta: B
Questão 2 (PM ES – Exatus 2013). Um caneco em formato de hemisfério cujo raio interno mede 20 cm é utilizado para transferir água de outro recipiente maior para copos em formato de cilindro circular reto, com raio da base medindo 4 cm e altura 15 cm. Considerando que esse caneco esteja com água equivalente a 4/5 do seu volume máximo, a água contida nele é suficiente para encher:
a) 13
b) 14
c) 10
d) 16
e) 17
Resolução
Volume do copo em formato de hemisfério:
Como ele tem formato de hemisfério, basta calcular o volume de uma esfera e dividir por 2:
Volume da esfera: V = π.r³.4/3 = π.20³.4/3 = 32000π/3
Volume do copo = 32000π/3 / 2 = 16000π/3
O problema nos fala que o copo estava com 4/5 da capacidade:
16000π/3 x 4/5 = 12800.π/3
Volume dos copos em formato de cilindro:
Volume do cilindro = altura x π.r² = 15.π.4² = 240π
Dividindo os dois volumes, o π é cancelado e temos 17,7777 copos
Resposta: E
Questão 3 (PM ES – Exatus 2013). Dados um cilindro circular reto e um cone circular reto de mesma altura e mesmo raio, é correto afirmar que o volume do cone é igual a:
a) três vezes o volume do cilindro
b) duas vezes o volume do cilindro
c) metade do volume do cilindro
d) terça parte do volume do cilindro
e) sexta parte do volume do cilindro
Resolução:
Fórmula para cálculo de volume de cilindros
V = π.r².h
Fórmula para cálculo de volume de cones
V = (π.r².h)/3
Como altura e raio são iguais, claramente o volume do cone é 1/3 do volume do cilindro.
Resposta: D
Questão 4 (Sejus ES – 2013). A quantidade de certo líquido, correspondente a 3/4 de um litro, será colocado em um recipiente de modo que ele fique completamente cheio. Para isso foram selecionados 3 recipientes com formas geométricas e medidas internas descritas a seguir:
I. Um paralelepípedo reto retângulo de dimensões: comprimento 15 cm, largura 2,5 cm e altura 20 cm.
II. Um cilindro reto de raio da base 5 cm e altura 10 cm. (use π = 3)
III. Um cubo de aresta igual a 5 cm.
Dos 3 recipientes oferecidos, atende ao que foi proposto
(A) I e II, apenas.
(B) I, II e III.
(C) I, apenas.
(D) I e III, apenas.
(E) II e III, apenas.
Resolução
Sabe-se que 1 litro pode ser colocado em um recipiente de 1000cm³.
Então temos que descobrir se em algum dos 3 casos o volume é 3/4 disso, ou seja, se o volume é 750cm³.
I) Volume do paralelepípedo = comprimento x largura x altura = 15 x 2,5 x 20 = 750cm³
II) Volume do cilindro = área da base x altura = π.5².10 = 3.25.10 = 750cm³
III) Volume do cubo = lado³ = 5³ = 125cm³
Resposta: A
Espero que gostem dos nossos exercícios resolvidos sobre cilindros.
Saber Matemática, o melhor site de matemática para concursos.
