Procurando exercícios resolvidos sobre os sólidos de revolução? Confira aqui várias questões comentadas, todas retiradas dos últimos concursos públicos.
Não deixe de ver também nossos exercícios resolvidos sobre os outros tópicos da geometria espacial.
Bom estudo!
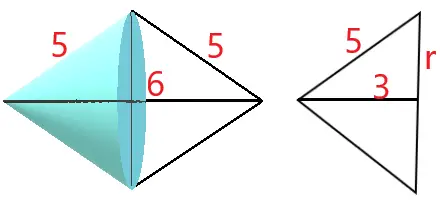
Questão 1 (PM ES – Exatus 2013). O volume do sólido gerado pela rotação de um triângulo isósceles de lados congruentes medindo 5 cm e base medindo 6 cm, em torno da base é igual a:
a) 32π cm³
b) 13π cm³
c) 14π cm³
d) 15π cm³
e) 16π cm³
Resolução
Veja na figura abaixo que, após a rotação em torno da base do triângulo isósceles, teremos um sólido formado por dois cones iguais.
Calcularemos o volume de um deles, e depois multiplicaremos por 2.
Utilizaremos o Teorema de Pitágoras para o cálculo do raio da base do cone:
5² = 3² + r²
25 = 9 + r²
r² = 25 – 9
r² = 16
r = √16
Calculando o volume do cone:
V = Área da base x altura / 3
V = π . 4² . 3 / 3
V = π . 16
V = 16π cm³
Volume total:
2 . 16π = 32π cm³
Resposta: A
Questão 2 (SEE AC – Funcab 2010). No ensino de geometria, nas séries iniciais, tem sua importância social o reconhecimento do universo tridimensional. Pensando nisso, uma professora levou para uma de suas aulas os objetos abaixo:
I. Uma caixa de sapato (paralelepípedo).
II. Uma lata de leite em pó (cilindro).
III. Uma bola de futebol (esfera).
Os sólidos acima são, respectivamente:
a) poliedro, sólido de revolução e poliedro.
b) sólido de revolução, poliedro e poliedro.
c) sólido de revolução, sólido de revolução e poliedro.
d) poliedro, sólido de revolução e sólido de revolução.
e) sólido de revolução, sólido de revolução e sólido de revolução.
Resolução
I – o paralelepípedo é um tipo de poliedro, que é um sólido geométrico de três dimensões, cuja superfície é formada por um número finito de superfícies planas.
II – um cilindro reto é um sólido de revolução, gerado pela rotação de um retângulo em torno de um de seus lados.
III – uma esfera é um sólido de revolução gerado pela rotação de um semicírculo em torno de um eixo que contém o diâmetro.
Resposta: D
Gostou dos nossos exercícios resolvidos sobre sólidos de revolução?
Deixe o seu comentário abaixo.