Procurando exercícios resolvidos sobre volumes de sólidos geométricos?

Chegou ao site certo.

Confira aqui uma seleção especial com várias questões comentadas, retiradas de concursos realizados por todo o Brasil.

 

 

Questão 1 (PM ES – Exatus 2013). Um caneco em formato de hemisfério cujo raio interno mede 20 cm é utilizado para transferir água de outro recipiente maior para copos em formato de cilindro circular reto, com raio da base medindo 4 cm e altura 15 cm. Considerando que esse caneco esteja com água equivalente a 4/5 do seu volume máximo, a água contida nele é suficiente para encher quantos copos?

a) 13

b) 14

c) 10

d) 16

e) 17

 

Resolução

Volume do copo em formato de hemisfério:

Como ele tem formato de hemisfério, basta calcular o volume de uma esfera e dividir por 2:

Volume da esfera: V = π.r³.4/3 = π.20³.4/3 = 32000π/3

Volume do copo = 32000π/3 / 2 = 16000π/3

 

A questão informa que o copo estava com 4/5 da capacidade:

16000π/3 x 4/5 = 12800.π/3

 

Volume dos copos em formato de cilindro:

Volume do cilindro = altura x π.r² = 15.π.4² = 240π

Dividindo os dois volumes, o π é cancelado e temos 17,7777 copos

 

Resposta: E

 

 

Questão 2 (PM ES – Exatus 2013). Um estoquista, ao conferir a quantidade de determinado produto embalado em caixas cúbicas de arestas medindo 40 cm, verificou que o estoque do produto estava empilhado de acordo com a figura que segue:

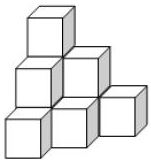
Ao realizar corretamente os cálculos do volume dessa pilha de caixas, o resultado obtido foi:

a) 0,64 m³

b) 1,6 m³

c) 6,4 m³

d) 16 m³

e) 64 m³

 

Resolução:

Temos 10 caixas cúbicas de 40 cm de aresta.

Sabe-se que 40cm = 0,4m

Cada caixa possui volume de 0,4×0,4×0,4 = 0,064 m³

Como temos 10 caixas: 10 x 0,064 = 0,64 m³

 

Resposta: A

 

 

Questão 3 (PM ES – Exatus 2013). Dados um cilindro circular reto e um cone circular reto de mesma altura e mesmo raio, é correto afirmar que o volume do cone é igual a:

a) três vezes o volume do cilindro

b) duas vezes o volume do cilindro

c) metade do volume do cilindro

d) terça parte do volume do cilindro

e) sexta parte do volume do cilindro

 

Resolução:

Fórmula para cálculo de volume de cilindros

V = π.r².h

Fórmula para cálculo de volume de cones

V = (π.r².h)/3

Como altura e raio são iguais, o volume do cone é 1/3 do volume do cilindro.

 

Resposta: D

 

 

Questão 4 (PM ES – Funcab 2013). Polícia Militar apreende mais de 3 kg de pasta base de cocaína em Linhares Em uma mochila foram apreendidos 84 tabletes plastificados de cocaína e um tablete grande medindo 20 x 10 cm da mesma substância, totalizando cerca de 3 quilos de cocaína, e R$ 91,00 em espécie. Caso o tablete grande mencionado tenha o formato de um paralelepípedo reto retângulo com 6 cm de altura, o valor do volume total de cocaína desse tablete, em cm³, será de:

A) 400

B) 600

C) 800

D) 1.000

E) 1.200

 

Resolução:

O tablete possui 20 cm de comprimento, 10 cm de largura e 6 cm de altura.

Volume = 20 x 10 x 6 = 1200 cm³

 

Resposta: E

 

 

Questão 5 (PM ES – Exatus 2013). Supondo as dimensões internas de cada pino plástico utilizado na embalagem de cocaína como sendo um cilindro de raio 0,5 cm e altura 4 cm, o valor do volume total de cocaína, desse pino plástico, completamente cheio, em cm³, será de:

(Adote o valor aproximado de π= 3 )

A) 2,5

B) 3

C) 3,5

D) 4

E) 4,5

 

Resolução:

Vamos utilizar a fórmula para calculo de volume do cilindro:

Volume = π . raio² . altura = π.0,5².4 = 3.0,25.4 = 3

 

Resposta: B

 

 

Questão 6 (Sejus ES – Vunesp 2013). A quantidade de certo líquido, correspondente a 3/4 de um litro, será colocado em um recipiente de modo que ele fique completamente cheio. Para isso foram selecionados 3 recipientes com formas geométricas e medidas internas descritas a seguir:

I. Um paralelepípedo reto retângulo de dimensões: comprimento 15 cm, largura 2,5 cm e altura 20 cm.

II. Um cilindro reto de raio da base 5 cm e altura 10 cm. (use π = 3)

III. Um cubo de aresta igual a 5 cm.

 

Dos 3 recipientes oferecidos, atende ao que foi proposto

(A) I e II, apenas.

(B) I, II e III.

(C) I, apenas.

(D) I e III, apenas.

(E) II e III, apenas.

 

Resolução:

Temos que 1 litro pode ser colocado em um recipiente de 1000cm³

Então temos que descobrir se em algum dos 3 casos o volume é ¾ disso, ou seja, se o volume é 750cm³

I) Volume do paralelepípedo = comprimento x largura x altura = 15 x 2,5 x 20 = 750cm³

II) Volume do cilindro = área da base x altura =  π.5².10 = 3.25.10 = 750cm³

III) Volume do cubo = lado³ = 5³ = 125cm³

 

Resposta: A

 

 

Questão 7 (Bombeiros ES – Cespe 2011). Uma caixa-d’água tem formato de um paralelepípedo retângulo, e outra, de um cilindro circular. A caixa-d’água com formato de paralelepípedo tem base igual a 20 m e 15 m, e altura igual a 5 m. O raio da base da caixa com formato cilíndrico mede 10 m, e a altura, 5 m. Tomando 3,14 como o valor aproximado da constante π, julgue os itens a e b:

 

a) A caixa com formato de paralelepípedo tem mais capacidade de armazenamento de água que a caixa com formato cilíndrico.

Resolução:

Volume do paralelepípedo = L X C X A = 20 x 15 x 5 = 1500 m³

Resposta: ERRADO

 

b) A caixa com formato cilíndrico tem capacidade de 1.570 m³.

Volume do cilindro = A X π X r² =5 x 3,14 x 10² = 5 x 3,14 x 100 = 1570 m³

Resposta: CERTO

 

 

Questão 8 (Bombeiros ES – Cespe 2011). Em uma unidade do Corpo de Bombeiros, os três reservatórios utilizados para armazenamento de água têm, respectivamente, os formatos cúbico, cilíndrico e cônico. O cubo tem arestas iguais a 1 m, o cilindro e o cone têm alturas iguais a 1 m, os raios das bases do cilindro e do cone são iguais a 0,5 m e o cone é circular reto. Considerando 3,14 o valor aproximado de π e desprezando as espessuras dos reservatórios, julgue os itens a e b:

 

a) A capacidade do reservatório cilíndrico é 78,5% da capacidade do reservatório cúbico.

Resolução

Volume do cubo = 1³ = 1 m³

Volume do cilindro =  π x r² x altura =  3,14 x 0,5² x 1 = 3,14 x 0,25 = 0,785 m³

Resposta: CERTO

 

b) A capacidade do reservatório cilíndrico é 3 vezes a capacidade do reservatório cônico.

Resolução

Basta observar as fórmulas dos volumes.

Cilindro =  π x r² x altura

Cone =  π x r² x altura / 3

Resposta: CERTO

 

 

Questão 9 (PRF – Cespe 2008). Considere que um cilindro circular reto seja inscrito em um cone circular reto de raio da base igual a 10 centímetros e a altura igual a 25 centímetros, de forma que a base do cilindro esteja no mesmo plano da base do cone. Em face dessas informações e, considerando, ainda, que h e r correspondam à altura e ao raio da base do cilindro, respectivamente, assinale a opção correta.

a) A função afim que descreve h como função de r é crescente.

b) O volume do cilindro como uma função de r é uma função quadrática.

c) Se A(r) é a área lateral do cilindro em função de r, então A(r) = 50.π.r.(1 – r/10)

d) É possível encontrar um cilindro de raio da base igual a 2 centímetros e altura igual a 19 centímetros que esteja inscrito no referido cone.

e) O cilindro de maior área lateral que pode ser inscrito no referido cone tem raio da base superior a 6 centímetros.

 

Resolução

Veja na figura que o cilindro está dentro do cone.

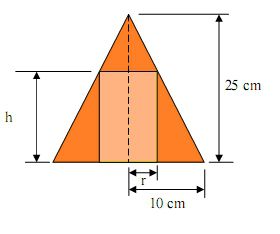
Vamos agora analisar cada uma das alternativas.

 

a) A função afim que descreve h como função de r é crescente.

Basta verificar que a medida que r aumenta, h diminui, ou seja, a função é decrescente.

Para encontrar a equação de h, vamos usar o método dos triângulos proporcionais. Se o triângulo maior, ABC, e o triângulo menor CDE. Veja:

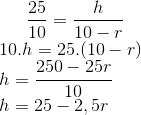
(o fato de -2,5r ser negativo nos prova que a função afim é decrescente)

 

b) O volume do cilindro como uma função de r é uma função quadrática.

V = π.r².h =  π.r².(25 – 25r/10) = 25π.r² – 25π.r³/10

Veja que a função é cúbica e não quadrática.

 

c) Se A(r) é a área lateral do cilindro em função de r, então A(r) = 50 r.

A(r) = base.altura = 2π.r.h = 2π.r.(25 – 25r/10) = 50π.r (1 – r/10)

 

d) É possível encontrar um cilindro de raio da base igual a 2 centímetros e altura igual a 19 centímetros que esteja inscrito no referido cone.

h = 25 – 25r/10 = 25 – 25.2/10 = 25 – 5 = 20

 

e) O cilindro de maior área lateral que pode ser inscrito no referido cone tem raio da base superior a 6 centímetros.

A(r) = 50π.r (1 – r/10) = 50π.r – 5π.r².    (função quadrática decrescente, o ponto máximo de r é o vértice)

xv = -b/2a – -50π/2(-5π) = 5

 

Resposta: C