Confira aqui vários exercícios resolvidos sobre análise combinatória, todos retirados dos mais diversos concursos públicos aplicados no Brasil.

Trata-se de uma matéria muito extensa, por isso recomendamos que o aluno acesse primeiro as nossas páginas sobre o assunto.

Bom estudo!

Questão 1 (PM SC – Cesiep 2011). Em uma corrida com 10 atletas competindo pergunta-se: de quantos modos distintos (combinações) podem ser conquistadas as medalhas de Ouro, Prata e Bronze?

a) 800

b) 1000

c) 720

d) 300

Resolução

Considerando que a ordem importa, temos um arranjo simples com 10 atletas, tomados 3 a 3:

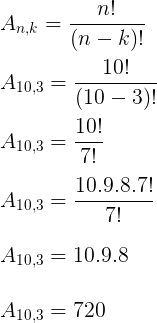
Resposta: C

Questão 2 (TRT ES – CESPE 2013). Considerando que, na fruteira da casa de Pedro, haja 10 uvas, 2 maçãs, 3 laranjas, 4 bananas e 1 abacaxi, julgue os próximos itens.

a) Há mais de 1.330 maneiras distintas de Pedro escolher pelo menos uma fruta entre aquelas que estão em sua fruteira.

Resolução

Pedro vai escolher algumas frutas. Ele tem a opção de pegar uma, duas ou várias.

Vamos analisar quantas opções ele tem para cada fruta:

• Uva: Pode pegar de 0 a 10, ou seja, 11 opções.
• Maçã: Pode pegar de 0 a 2, ou seja, 3 opções.
• Laranja: Pode pegar de 0 a 3, ou seja, 4 opções.
• Banana: Pode pegar de 0 a 4, ou seja, 5 opções.
• Abacaxi: Pode pegar 0 ou 1, ou seja, 2 opções.

Total de opções: 11 x 3 x 4 x 5 x 2 = 1320

Basta descontar a possibilidade de Pedro não pegar nenhuma fruta:

1320 – 1 = 1319

Há 1319 maneiras distintas, ou seja, menos de 1330.

Resposta: ERRADO

b) Se, para fazer uma salada de frutas, Pedro deve escolher pelo menos dois tipos de frutas, em qualquer quantidade, então há menos de 1.000 maneiras distintas de Pedro escolher frutas para compor sua salada.

Resolução

Na letra b vimos que ele tem 1319 opções para escolher pelo menos uma.

O que muda quando falamos em ‘pelo menos duas’ é que devemos descartar as opções que ele teria de escolher uma fruta apenas.

Para pegar apenas uva uma ele tem 10 opções. Apenas uma, apenas duas, apenas três, …, ou todas as 10 uvas.

Da mesma forma, duas opções pegando apenas maçãs, 3 para apenas laranjas, 4 para apenas bananas e uma para o abacaxi.

Total:

10 + 2 + 3 + 4 + 1 = 20 opções

Temos:

1319 – 20 = 1299 opções

Há 1299 maneiras distintas, ou seja, mais de 1000.

Resposta: ERRADO

c) Se Pedro desejar comer apenas bananas, haverá quatro maneiras de escolher algumas frutas para comer.

Resolução

Se ele quer apenas bananas, ele poderia pegar uma, duas, três ou quatro, ou seja, ele tem 4 opções.

Resposta: CERTO

Obs: A questão pode ter outra interpretação, repare que ele vai escolher algumas frutas, ou seja, poderíamos eliminar a opção de comer apenas uma banana e ter apenas 3 opções.

d) Se Pedro desejar comer apenas um tipo de fruta, a quantidade de maneiras de escolher frutas para comer será superior a 100.

Resolução

• Se ele comer apenas Uva ele terá 10 opções
• Se ele comer apenas Maçã ele terá 2 opções
• Se ele comer apenas Laranja ele terá 3 opções
• Se ele comer apenas Banana ele terá 4 opções
• Se ele comer apenas Abacaxi ele terá apenas 1 opção

Total de 20 opções, ou seja, inferior a 100.

Resposta: ERRADO

Questão 3 (PF – CESPE 2012). Dez policiais federais — dois delegados, dois peritos, dois escrivães e quatro agentes — foram designados para cumprir mandado de busca e apreensão em duas localidades próximas à superintendência regional. O grupo será dividido em duas equipes. Para tanto, exige-se que cada uma seja composta, necessariamente, por um delegado, um perito, um escrivão e dois agentes.

Considerando essa situação hipotética, julgue os itens que se seguem.

a) Se todos os policiais em questão estiverem habilitados a dirigir, então, formadas as equipes, a quantidade de maneiras distintas de se organizar uma equipe dentro de um veículo com cinco lugares — motorista e mais quatro passageiros — será superior a 100.

Resolução

Temos uma permutação de 5 pessoas (5 pessoas e 5 lugares para sentar).

P_n = n!

P₅ = 5!

P₅ = 5.4.3.2.1

P₅ = 120 maneiras

Resposta: CERTO

b) Há mais de 50 maneiras diferentes de compor as referidas equipes.

Resolução

Temos

• duas opções para delegados
• duas opções para peritos
• duas opções para escrivães
• duas entre quatro opções para agentes

Para escolher os dois agentes temos uma combinação de 4, tomados 2 a 2:

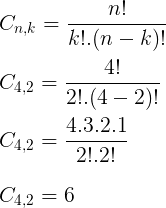
Total: 2 x 2 x 2 x 6 = 48

Resposta: ERRADO

Questão 4 (BB – Cesgranrio 2010). Uma artesã de bijuterias fabrica um colar de contas no qual utiliza 16 contas pequenas e duas contas grandes, cujo modelo é apresentado abaixo.

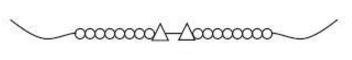
Os critérios que ela utiliza para montar cada colar são os seguintes:

• as contas pequenas são todas da mesma cor;
• contas grandes devem ter cores diferentes;
• se as contas pequenas forem da cor “x”, nenhuma conta grande pode ser da cor “x”.

Sabendo-se que a artesã dispõe de contas pequenas brancas, pretas, azuis e laranjas e de contas grandes brancas, vermelhas, verdes, azuis e rosas, de quantos modos distintos ela pode escolher as cores das contas que irão compor um colar?

a) 28

b) 30

c) 32

d) 40

e) 42

Resolução

Cores para as contas pequenas: branca, preta, azul e laranja

Cores para as contas grandes: branca, vermelha, verde, azul e rosa

Se escolhermos branca ou azul para as contas pequenas, cores comuns as duas, para escolhermos as cores das contas grandes teremos uma combinação de 2 em 4, logo:

2 x C(2,4) = 2 x 6 = 12

Se escolhermos preta ou laranja para as contas pequenas, cores que não podem ser usadas nas contas grandes, para escolhermos as cores das contas grandes teremos uma combinação de 2 em 5, logo:

2 x C(2,5) = 2 x 10 = 20

Total: 12 + 20 = 32

Resposta: C

Questão 5 (TRT ES – CESPE 2009). Em 2007, no estado do Espírito Santo, 313 dos 1.472 bacharéis em direito que se inscreveram no primeiro exame do ano da Ordem dos Advogados do Brasil (OAB) conseguiram aprovação. Em 2008, 39 dos 44 bacharéis provenientes da Universidade Federal do Espírito Santo (UFES) que fizeram a primeira fase do exame da OAB foram aprovados.

Com referência às informações contidas nos textos acima, julgue a seguinte afirmação:

“Com relação à primeira fase do exame da OAB de 2008, caso se deseje formar uma comissão composta por 6 bacharéis provenientes da UFES, sendo 4 escolhidos entre os aprovados e 2 entre os reprovados, haverá mais de 9 × 10^5 maneiras diferentes de se formar a referida comissão.”

Resolução

Temos uma combinação de 4 em 39 para os aprovados e uma combinação de 2 em 5 para os reprovados.

C4,39 x C2,5

C4,39 = 39!/[4!.(39-4)!]= 39!/4!.35! = 39.38.37.36/4.3.2.1 = 82251

C2,5 = 5!/[2!.(5-2)!] = 5!/2.3! = 5.4/2 = 10

C4,39 x C2,5 = 82251 x 10 = 822510 = 8,2 x 10^5 < 9,5 x 10^5

Resposta: ERRADO

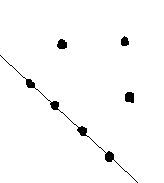
Questão 6 (RFB – ESAF 2009). Sabe-se que os pontos A,B,C, D, E, F e G são coplanares, ou seja, estão localizados no mesmo plano. Sabe-se, também, que destes sete pontos, quatro são colineares, ou seja, estão numa mesma reta. Assim, o número de retas que ficam determinadas por estes sete pontos é igual a:

a) 16

b) 28

c) 15

d) 24

e) 32

Resolução

Vejamos na figura abaixo como estão dispostos os pontos:

A questão pode ser resolvida de duas formas distintas:

Resolução 1

Temos que dois pontos bastam para determinar uma reta, então basta fazer a combinação dos 7 pontos tomados 2 a 2, subtraindo a combinação dos 4 pontos (colineares) tomados 2 a 2, somando a reta que passa pelos 4 pontos colineares.

C7,2 – C4,2 + 1 = 7!/(7-2)!2! – 4!/(4-2)!2! + 1 = 21 – 6 + 1 = 16

Resolução 2

Cada um dos 3 pontos não colineares pode ser ligado nos 4 pontos colineares, ou seja, cada um forma 4 retas, daí, temos 3 x 4 = 12 retas.

Podemos também formar 3 retas utilizando apenas os 3 pontos não colineares.

Por último, uma reta que passa pelos 4 pontos colineares.

Logo, 12 + 3 + 1 = 16

Resposta: A

Gostou dos nossos exercícios resolvidos sobre análise combinatória?

Deixe o seu comentário.