QUESTÃO 164. Um artista plástico esculpe uma escultura a partir de um bloco de madeira de lei, em etapas. Inicialmente, esculpe um cone reto com 36 cm de altura e diâmetro da base medindo 18 cm. Em seguida, remove desse cone um cone menor, cujo diâmetro da base mede 6 cm, obtendo, assim, um tronco de cone, conforme ilustrado na figura.
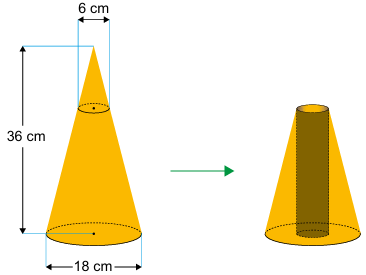
Em seguida, perfura esse tronco de cone, removendo um cilindro reto, de diâmetro 6 cm, cujo eixo de simetria é o mesmo do cone original. Dessa forma, ao final, a escultura tem a forma de um tronco de cone com uma perfuração cilíndrica de base a base.
O tipo de madeira utilizada para produzir essa escultura tem massa igual a 0,6 g por centímetro cúbico de volume. Utilize 3 como aproximação para π.
Qual é a massa, em grama, dessa escultura?
A) 1 198,8
B) 1 296,0
C) 1 360,8
D) 4 665,6
E) 4 860,0
Resolução
O nosso primeiro objetivo será calcular a altura (x) do cone menor. Utilizaremos uma sessão ortogonal no cone maior, gerando dois triângulos semelhantes, onde será possível calcular o valor de x.
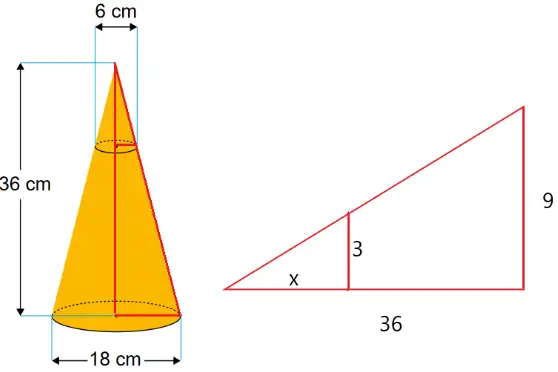
36/9 = x/3
x/3 = 4
x = 12
Sabendo que a altura do cone menor é igual a 12 cm, e considerando que o cone maior possui altura igual a 36 cm, podemos concluir que o tronco de cone e o cilindro reto possuem altura igual a 24 cm.
Como o nosso objetivo é calcular o volume da escultura, precisaremos fazer a seguinte conta:
(Volume do cone maior) – (volume do cone menor) – (volume do cilindro reto)
Utilizaremos as fórmulas do volume do cone (V = π.r².h/3) e do volume do cilindro (V = π.r².h).
Considere que o cone maior possui raio igual a 9 cm e altura igual a 36 cm, o cone menor possui raio igual a 3 cm e altura igual a 12 cm, e o cilindro possui raio igual a 3 cm e altura igual a 24 cm.
π.9².36/3 – π.3².12/3 – π.3².24
π.81.12 – π.9.4 – π.9.24
972π – 36π – 216π
720π
Utilizando 3 como aproximação para π, o volume da escultura é igual a:
720.3 = 2160 cm³
O tipo de madeira utilizada para produzir essa escultura tem massa igual a 0,6 g por centímetro cúbico de volume.
2160 . 0,6 = 1296 g
Resposta: B
