Confira aqui vários exercícios resolvidos sobre a função polinomial, todos retirados das últimas provas de concursos realizados pelo país.
Bom estudo!
Exercício 1 (Marinha). Encontre os valores absolutos máximo e mínimo, respectivamente, da função polinomial f(x) = x³ – 3x² + 2, -1/2 ≤ x ≤ 4, e assinale a opção correta:
a) 17 e -3
b) 18 e 9/8
c) 17 e -2
d) 18 e -2
e) 19 e 1
Resolução
A primeira derivada de uma função polinomial nos fornece o coeficiente angular da reta tangente, assim nos pontos onde f'(x) = 0, teremos um máximo ou mínimo local.
f'(x) = 3x² – 6x
3x² – 6x = 0
3x(x – 2) = 0
Daí, as raízes de f’ são x = 0 e x = 2.
A segunda derivada nos fornece a informação sobre a concavidade da função.
f”(x) = 6x – 6
f”(x) > 1, côncava para cima;
f”(x) < 1, côncava para baixo.
Sabendo dessas informações, podemos construir o seguinte gráfico da função polinomial f:
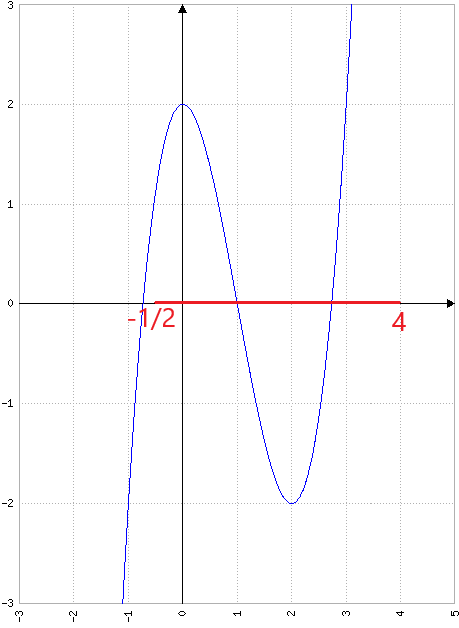
Observando o gráfico, é possível observar que os valores absolutos máximo e mínimo, respectivamente, no intervalo -1/2 ≤ x ≤ 4, são f(4) e f(2):
f(4) = 4³ – 3.4² + 2 = 64 – 48 + 2 = 18
f(x) = 2³ – 3.2² + 2 = 8 – 12 + 2 = -2
Resposta: D
Exercício 2 (Aeronáutica). No gráfico abaixo estão representadas as funções f:R→R e g:R→R.
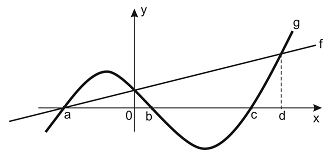
Sobre estas funções é correto afirmar que:

Analisando cada uma das alternativas:
a) FALSA. Observe no gráfico que existe c, com 0<c<d, onde g(x)/f(x)>0, para c<x<d.
b) FALSA. Observe no gráfico que f(x)>g(x) também quando x<a.
c) FALSA. Observe que f(a) = 0 e g(c) = 0, ou seja, devemos verificar se g(0)/f(d)>1. Claramente temos que f(d)>g(0), logo, g(0)/f(d)<1.
d) VERDADEIRA. Como temos um produto f(x).g(x) e queremos saber quando este produto é maior ou igual a zero, basta observarmos os intervalos onde as duas funções possuem o mesmo sinal, fazendo com que o produto não seja negativo. Isto ocorre para x≤b ou x≥c.
Resposta: D
Exercício 3 (Cesgranrio). Considere as funções polinomiais f(x) = x2 + 6x – 16 e g(x) = 3x – 9. Se g(m) = f(– 1), então m é igual a
a) -4
b) -3
c) -2
d) -1
e) 0
Resolução
Calculando os valores de f(-1) e g(m), temos:
f(-1) = (-1)2 + 6(-1) – 16 = 1 – 6 – 16 = -21
g(m) = 3m – 9
Considerando que g(m) = f(– 1):
3m – 9 = -21
3m = – 21 + 9
3m = -12
m = -12/3
m = -4
Resposta: A
Gostou dos nossos exercícios resolvidos sobre função polinomial?
Deixe o seu comentário.
