Confira aqui tudo o que você precisa saber sobre um sistema de inequações do 1° (primeiro) grau, onde apresentaremos a definição e como é feita a resolução, com vários exemplos.
É importante que o aluno tenha conhecimento prévio acerca das inequações e sistema de equações do 1° grau.
Bom estudo!
Definição
Um sistema de inequações do 1° grau é um conjunto por duas ou mais inequações de grau 1, com uma variável.
A solução deve satisfazer a todas as desigualdades apresentadas no sistema.
Exemplos:
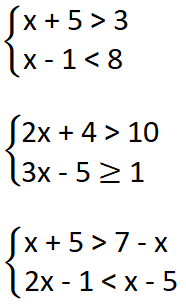
Como resolver um sistema de inequações do 1° grau
A resolução de um sistema de equações é feita primeiramente através da resolução isolada de cada uma das inequações.
O resultado final será a intersecção dos conjuntos solução encontrados.
Veremos agora como é feita a resolução de um sistema de inequações na prática, onde descobriremos o conjunto solução de cada um dos sistemas apresentados nos exemplos.
Resolução do primeiro sistema de inequações
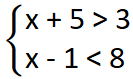
Resolvendo cada uma das inequações:
- Inequação 1
x + 5 > 3
x > 3 – 5
x > -2
S = {x ∈ R / x > -2}
- Inequação 2
x – 1 < 8
x < 8 + 1
x < 9
S = {x ∈ R / x < 9}
Veja que a solução do sistema são todos os valores maiores que -2 e menores que 9.
S = {x ∈ R / -2 < x < 9}
Resolução do segundo sistema de inequações
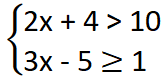
Resolvendo cada uma das inequações:
- Inequação 1
2x + 4 > 10
2x > 10 – 4
2x > 6
x > 6/2
x > 3
S = {x ∈ R / x > 3}
- Inequação 2
3x – 5 ≥ 1
3x ≥ 1 + 5
3x ≥ 6
x ≥ 6/3
x ≥ 2
S = {x ∈ R / x ≥ 2}
Veja que a solução do sistema são todos os valores maiores ou iguais a 2 e maiores que 3.
S = {x ∈ R / x > 3}
Resolução do terceiro sistema de inequações
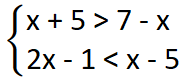
Resolvendo cada uma das inequações:
- Inequação 1
x + 5 > 7 – x
x + x > 7 – 5
2x > 2
x > 2/2
x > 1
S = {x ∈ R / x > 1}
- Inequação 2
2x – 1 < x – 5
2x – x < – 5 + 1
x < – 4
S = {x ∈ R / x < – 4}
Veja que a solução do sistema são todos os valores maiores que 1 e menores que -4.
Como não existem valores reais que atendem simultaneamente as duas condições, o conjunto solução é vazio.
S = { }
Aprendeu a resolver um sistema de inequações do 1° grau?
Deixe o seu comentário.
