O número de Euler é recebeu este nome em homenagem ao matemático Leonhard Euler. Trata-se de um número irracional e positivo, além de ser a base dos logaritmos naturais.
Como todo número irracional, o número de Euler possui infinitas casas decimais e nenhum padrão. O símbolo utilizado para representá-lo é a letra e.
Veja abaixo o número de Euler com 1000 casas decimais:
2,7182818284
5904523536 0287471352 6624977572 4709369995 9574966967 6277240766 3035354759 4571382178 5251664274 2746639193 2003059921 8174135966 2904357290 0334295260 5956307381 3232862794 3490763233 8298807531 9525101901 1573834187 9307021540 8914993488 4167509244 7614606680 8226480016 8477411853 7423454424 3710753907 7744992069 5517027618 3860626133 1384583000 7520449338 2656029760 6737113200 7093287091 2744374704 7230696977 2093101416 9283681902 5515108657 4637721112 5238978442 5056953696 7707854499 6996794686 4454905987 9316368892 3009879312 7736178215 4249992295 7635148220 8269895193 6680331825 2886939849 6465105820 9392398294 8879332036 2509443117 3012381970 6841614039 7019837679 3206832823 7646480429 5311802328 7825098194 5581530175 6717361332 0698112509 9618188159 3041690351 5988885193 4580727386 6738589422 8792284998 9208680582 5749279610 4841984443 6346324496 8487560233 6248270419 7862320900 2160990235 3043699418 4914631409 3431738143 6405462531 5209618369 0888707016 7683964243 7814059271 4563549061 3031072085 1038375051 0115747704 1718986106 8739696552 1267154688 9570350354 …
Aplicações à Matemática Financeira
Imagine uma aplicação, onde você deposita R$ 1,00, com rendimento de 100% ao ano.
100% de R$ 1,00 = R$ 1,00
Após um ano, o saldo final será de R$ 2,00.
Mas o que aconteceria se o rendimento fosse de 50% ao semestre, pelo mesmo período de 1 ano?
- Após o 1º semestre: R$ 1,00 + 50% = R$ 1,50
- Após o 2º semestre: R$ 1,50 + 50% = R$ 2,25
E se o rendimento fosse de 25% ao trimestre, e também pelo prazo total de 1 ano?
- Após o 1º trimestre: R$ 1,00 + 25% = R$ 1,25
- Após o 2º trimestre: R$ 1,25 + 25% = R$ 1,5625
- Após o 3º trimestre: R$ 1,5625 + 25% = R$ 1,953125
- Após o 4º trimestre: R$ 1,953125 = 25% = R$ 2,44140625
Inicialmente, temos a ideia de que o valor sempre será maior. Isto não deixa de ser verdade, mas ele tem um limite. Veja o que acontece quando capitalizamos os juros com uma frequência maior:
| Período | Total (aproximado) |
| Ano | R$ 2,00000 |
| Semestre | R$ 2,25000 |
| Trimestre | R$ 2,44141 |
| Mês | R$ 2,61304 |
| Semana | R$ 2,69260 |
| Dia | R$ 2,71457 |
| Hora | R$ 2,71813 |
| Minuto | R$ 2,71828 |
| Segundo | R$ 2,71828 |
Perceba que o aumento passa a ser irrelevante a partir de certo ponto. Cada vez que o cálculo é feito com um período de capitalização menor, mais o resultado se aproxima do número e.
Analisando o exemplo acima e a fórmula para o cálculo do montante em juros compostos, temos que o número de Euler pode ser calculado através do limite abaixo:
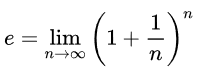
OUTRAS FORMAS DE CALCULARMOS O NÚMERO DE EULER
- Substituindo n = 1/h no limite anterior:
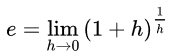
- Série de Taylor:
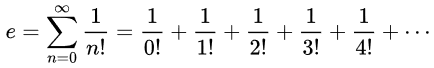
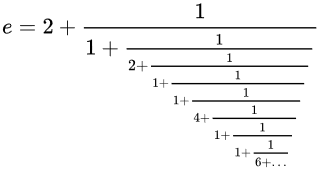
- Desenvolvimento da fração:
Gostou da nossa publicação sobre o fascinante número de Euler?
Deixe o seu comentário.