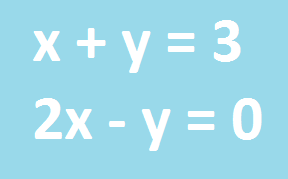Vamos aprender a resolver sistemas de equações do 1° (primeiro) grau (sistemas lineares)? Nesta página vamos estudar basicamente a resolução de sistemas de equações que envolvem duas equações e duas incógnitas.
Salientamos que quando existem 3 ou mais equações/incógnitas o sistema também pode ser resolvido pelos métodos a serem apresentados, porém existem outras formas mais eficientes.
Bom estudo!
INTRODUÇÃO
Resolver um sistema de equações consiste em achar os valores das incógnitas que satisfazem simultaneamente as duas equações do sistema.
Veja o exemplo:
x + y = 9
x – y = 1
É fácil notar que se tomarmos x = 5 e y = 4, ambas as igualdades estarão satisfeitas. Logo, x = 5 e y = 4 são as soluções do sistema linear proposto.
A seguir, vamos apresentar os dois métodos práticos para resolução de sistemas.
MÉTODO DA SUBSTITUIÇÃO
Consiste em colocar uma das incógnitas em função da outra e substituir na segunda equação.
Vamos ao exemplo:
Resolver o sistema:
2x + 3y = 7
5x – 4y = 6
Por este método, vamos tomar a primeira equação e escrever x em função de y:
2x = 7 – 3y
x = (7 – 3y) / 2
Agora vamos substituir o valor de x na segunda equação:
5.(7 – 3y) / 2 – 4y = 6
2.5.(7 – 3y) / 2 – 2.4y = 2.6
5.(7 – 3y) – 8y = 12
35 – 15y – 8y = 12
– 23y = 12 – 35
– 23y = -23
y = 1
Achando o valor de y, vamos utilizar a equação de x em função de y para acharmos o valor de x:
x = (7 – 3y) / 2
x = (7 – 3)/2
x = 4/2
x = 2
Logo, a solução é x = 2 e y = 1
MÉTODO DA ADIÇÃO
Consiste em eliminar uma das incógnitas, onde teríamos uma equação do primeiro grau, com apenas uma incógnita, que é simples de resolver.
Vamos ao exemplo:
Resolver o sistema:
2x + 3y = 7
5x – 4y = 6
Primeiramente, devemos relembrar que em uma equação isolada, podemos multiplicar toda ela por uma constante real que suas raízes não são alteradas.
Neste exemplo, nosso objetivo é eliminar a incógnita y. Note que se multiplicarmos a primeira por 4 e a segunda por 3 e somarmos as duas, a incógnita y será anulada.
8x + 12y = 28
15x -12y = 18
Somando as equações resultantes:
8x + 12y + 15x – 12y = 28 + 18
23x = 46
x = 46/23 = 2
Para achar o valor de y, basta escolher uma das equações iniciais e substituir x = 2:
2x + 3y = 7
2..2 + 3y = 7
4 + 3y = 7
3y = 7 – 4
3y = 3
y = 1
Logo, a solução é x = 2 e y = 1
CONSIDERAÇÃO FINAL
Além desses dois métodos, existem outros. Nosso objetivo foi apresentar os mais utilizados, de modo a não confundir a cabeça do estudante. Não existe método mais fácil ou mais difícil, vai depender de cada exemplo.
Aprendeu a resolver um sistema de equações do 1° grau?
Deixe o seu comentário.