Dando continuidade ao estudo da reta na geometria analítica, vamos falar um pouco sobre as retas paralelas.
Não deixe de ver também nossos conteúdos sobre os outros tópicos da geometria analítica.
Bom estudo!
Dizemos que duas retas são paralelas quando ocupam o mesmo plano e não possuem nenhum ponto em comum.
A linguagem matemática utilizada para informar que as retas r e s são paralelas é r ⁄ ⁄ s.
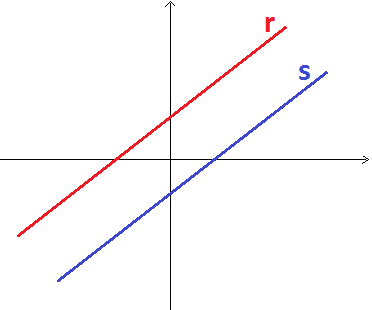
Na figura é possível observar que as retas são paralelas porque possuem a mesma inclinação, ou seja, possuem os mesmos coeficientes angulares.
Utilizando a linguagem matemática, temos que:
r ⁄ ⁄ s ⇔ α1 = α2
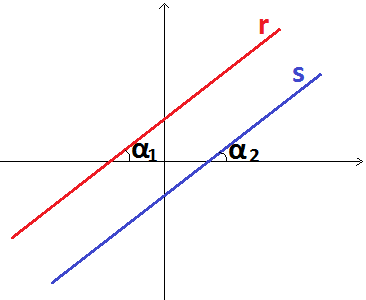
Conclusão: A maneira mais rápida de identificarmos duas retas paralelas é comparando o coeficiente angular. Caso sejam iguais, as retas serão paralelas, caso contrário, serão concorrentes.
Obs: Devemos descartar os casos onde os coeficientes angulares são iguais assim como as equações reduzidas das retas, pois neste caso as retas serão coincidentes.
Exemplo 1. Verificar se as retas r: x + 5y + 1 = 0 e s: 2x – y + 4 = 0 são paralelas.
Calculando o coeficiente angular de cada uma das retas:
Reta r
x + 5y + 1 = 0
5y = -x – 1
y = -x/5 – 1/5
m = -1/5
Reta s
2x – y + 4 = 0
y = 2x + 4
m = 2
Conclusão: Os coeficientes angulares das retas r e s são diferentes, ou seja, as retas NÃO são paralelas.
Exemplo 2. Verificar se as retas r: 3x – 2y + 6 = 0 e s: -6x + 4y + 10 = 0 são paralelas.
Calculando o coeficiente angular de cada uma das retas:
Reta r
3x – 2y + 6 = 0
2y = 3x + 6
y = (3x + 6) / 2
y = (3/2)x + 3
m = 3/2
Reta s
-6x + 4y + 10 = 0
4y = 6x – 10
y = (6x – 10) / 4
y = (6/4)x – 10/4
y = (3/2)x – 5/2
m = 3/2
Conclusão: As retas r e s possuem o mesmo coeficiente angular e são paralelas.
Exemplo 3. Determinar a equação geral da reta r que passa pelo ponto P(1, 1) e é paralela à reta s: 3x – y + 5 = 0.
Podemos determinar a equação da reta apenas conhecendo um de seus pontos e a inclinação. A questão nos informou que a reta r passa pelo ponto (1 ,1) e que deve ser paralela a reta s, ou seja, deve possuir a mesma inclinação. Nosso primeiro objetivo será calcular a inclinação (coeficiente angular) da reta s.
3x – y + 5 = 0
y = 3x + 5
m = 3
Como a reta s possui coeficiente angular igual a 3, este também deve ser o coeficiente angular da reta r.
Determinando a equação da reta r, sabendo que m = 3 e que (1, 1) ∈ r:
y – y0 = m(x – x0)
y – 1 = 3.(x – 1)
y – 1 = 3x – 3
3x – y – 3 + 1 = 0
3x – y – 2 = 0
Daí, a equação da reta que passa pelo ponto (1, 1) e que é paralela à reta 3x – y + 5 = 0 é 3x – y – 2 = 0.
Gostou do nosso conteúdo sobre retas paralelas?
Deixe o seu comentário e compartilhe nas redes sociais.