Estudando para o concurso de soldado da polícia militar de Tocantins (PM – TO)? Confira aqui a prova resolvida do último concurso, realizado em 2013 pela Consulplan.
21. Numa escola existem 41 salas das quais 22 possuem ar condicionado, 20 possuem ventilador e 5 não possuem ar condicionado nem ventilador. Quantas salas dessa escola possuem os dois tipos de aparelho?
(A) 4
(B) 6
(C) 7
(D) 9
Sendo:
x = quantidade de salas com ar condicionado, somente.
Y = quantidade de salas com ar condicionado e ventilador.
Z = quantidade de salas com ventilador, somente.
5 = quantidade de salas sem ar condicionado nem ventilador.
Com as informações do enunciado, temos:
(1) x + y + z + 5 = 41
(2) x + y = 22
(3) y + z = 20
Fazendo (1) – (3):
x + y + z + 5 – y – z = 41 – 20
x + 5 = 21
x = 16
Da equação (2):
x + y = 22
16 + y = 22
y = 6
Resposta: 6
22. Numa sessão de cinema, 2/5 do público presente é composto por crianças, 1/4 por adolescentes e o restante por adultos. Se a diferença entre o número de crianças e adultos é igual a 4, então quantos adolescentes compareceram a essa sessão?
(A) 16
(B) 20
(C) 24
(D) 28
Sendo x a fração que representa os adultos em relação ao total, temos:
2/5 + 1/4 + x = 1
(8 + 5)/20 + x = 1
13/20 + x = 1
x = 1 – 13/20
x = 7/20
Considerando agora k a quantidade total e sabendo que a diferença entre o número de crianças e adultos é igual a 4:
2k/5 – 7k/20 = 4
(8k – 7k)/20 = 4
k = 4.20
k = 80
Isso significa que a sessão tinha 80 pessoas.
Para calcularmos a quantidade de adolescentes, vamos utilizar a informação que esse número é 1/4 do total:
80 . 1/4 = 20
23. Cássio é dentista e atende, em média, um paciente a cada 20 minutos. Num certo dia, Cássio conseguiu atender 16 pessoas num intervalo de 4 horas e 16 minutos. Quantos minutos ele conseguiu economizar, em média, em cada atendimento?
(A) 2 minutos
(B) 3 minutos
(C) 4 minutos
(D) 6 minutos
Para calcularmos a média no dia citado, basta dividirmos o tempo gasto pela quantidade de atendimentos.
Vamos então transformar 4 horas e 16 minutos em uma fração, para que possamos efetuar a divisão:
4 + 16/60
4 + 4/15
(60 + 4)/15
64/15
Agora podemos dividir por 16 para calcularmos a média:
(64/15) / 16 = 64/15.16 = 64/240 = 16/60
Poderíamos ter simplificado a fração, porém nosso objetivo é calcular o tempo médio em horas de cada atendimento, por isso deixamos o denominador ser igual a 60. Podemos então dizer que o mesmo é 16/60 horas ou 16 minutos.
Tempo médio economizado por atendimento: 20 – 16 = 4
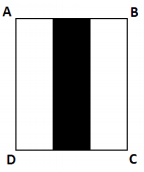
24. A Área em negrito da figura corresponde a 1/3 da Área do retângulo ABCD, cujo perímetro mede 40 cm. Considerando ainda que o perímetro da região em negrito equivale a 3/5 do perímetro do retângulo ABCD, então a Área desse retângulo mede
(A) 84 cm2.
(B) 90 cm2.
(C) 92 cm2.
(D) 96 cm2.
Sejam:
AB = DC = x
BC = DA = y
Como a área do retângulo em negrito é 1/3 da área de ABCD, temos que as medidas do retângulo em negrito são x/3 e y.
Sabendo que o perímetro de ABCD é 40, temos:
x + x + y + y = 40
2x + 2y = 40 (1)
Sabendo que o perímetro da região em negrito é 3/5 de ABCD, temos:
x/3 + x/3 + y + y = 40.3/5
2x/3 + 2y = 24 (2)
Fazendo (1) – (2):
2x + 2y – 2x/3 – 2y = 40 – 24
4x/3 = 16
x = 16.3/4
x = 12
Utilizando a equação (1) para calcularmos o valor de y:
2x + 2y = 40
2.12 + 2y = 40
24 + 2y = 40
2y = 40 – 24
2y = 16
y = 16/2
y = 8
Calculando a área de ABCD:
12.8 = 96
25. Marcelo tem quatro filhos, sendo duas meninas e dois meninos: Fabiana, Carolina, Diogo e Antônio. Considere que dois de seus filhos aniversariam hoje e são gêmeos e que:
– Carolina é um ano mais nova que Diogo e Antônio é quatro anos mais velho que Fabiana;
– Diogo é quatro anos mais novo que Antônio e Carolina é um ano mais nova que Fabiana;
– A soma das idades de Antônio e Carolina é igual a 19 anos.
Assim, é correto afirmar que
(A) Diogo é um dos gêmeos.
(B) Antônio é um dos gêmeos.
(C) Fabiana não é um dos gêmeos.
(D) os gêmeos possuem o mesmo sexo.
Sejam:
A = idade de Antônio
C = idade de Carolina
D = idade de Diogo
F = idade de Fabiana
Pela afirmação:
“Carolina é um ano mais nova que Diogo e Antônio é quatro anos mais velho que Fabiana”
C = D – 1
A = F + 4
Pela afirmação:
“Diogo é quatro anos mais novo que Antônio e Carolina é um ano mais nova que Fabiana”
A = D + 4
C = F – 1
Se analisarmos as duas equações:
C = D – 1
C = F – 1
Daí,
D – 1 = F – 1
D = F
Concluímos que a idade de Diogo e Fabiana são iguais, portanto são gêmeos.
Resposta: (A) Diogo é um dos gêmeos.

Olá
Na segunda questão por que você mutiplica de forma cruzada sendo que as frações a mutiplicação é o de cima vezes o de cima e o de baixo vezes o de baixo? Você obtem o número 8 que só pode ser encontrado através da mutiplicação – no caso – CRUZADA INCORRETA. Ademais- você menciona a seguinte
“x = 1 – 13/20
x = 7/20” Onde que 1-13 será 7 ???? A resposta correta seria 12/20. Me diga em quê estou errado!
é o seguinte vitor, se você analisar x=1-13/20 é o mesmo que 1/1-13-20, que no caso é feito a subtração das frações, onde o mmc dos denominadores 1 e 20 é 20, que no caso divide 20 por 1 e multiplica por 1, e depois divide 20 por 20 e multiplica por 13 = 20-13/20 = 7/20. sacou?!?!
eu gostaria de saber da onde saiu o número 20 nessa questão. (8+5)/20??? ALGUÉM ME EXPLICA POR FAVOR