Se preparando para concursos da Polícia Militar? Confira aqui a prova resolvida da PM do Pará realizado em 2007 pela Fundação de Amparo e Desenvolvimento da Pesquisa (Fadesp).

A prova foi de nível médio e teve algumas questões bem interessantes que merecem ser estudadas com atenção.

Boa sorte a todos!

 

 

16. Dos 100 soldados que participavam de um curso de formação de cabos, 40 gostavam de praticar voleibol, 68 gostavam de praticar futebol e 14 não gostavam de praticar esses esportes. A quantidade de soldados que gostavam de praticar tanto voleibol quanto futebol é igual a

(A) 18.

(B) 22.

(C) 30.

(D) 46.

 

Resolução

Vamos resolver a questão com o auxílio da figura abaixo, sendo que no círculo vermelho estão os soldados que gostam de voleibol, no verde os que gostam de futebol, e fora dos dois, os que não gostam de nenhum desses esportes.

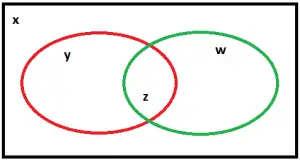
Temos:

x + y + z + w = 100

y + z = 40

z + w = 68

x = 14

 

Como x = 14, temos que:

x + y + z + w = 100

14 + y + z + w = 100

y + z + w = 100 – 14

y + z + w = 86

 

Assim, temos 3 equações:

(1) y + z + w = 86

(2) y + z = 40

(3) z + w = 68

 

Fazendo (1) – (2):

y + z + w – y – z = 86 – 40

y + z + w – y – z = 86 – 40

w  = 46

 

A questão pede para descobrirmos quantos gostam dos dois esportes, ou seja, o valor da letra z. Podemos utilizar a equação 3:

z + w = 68

z + 46 = 68

z = 68 – 46

z = 22

 

Resposta: B

 

 

17. Se numa festa a quantidade de moças está para a quantidade de rapazes na razão de 13 para 12, então a porcentagem de moças presentes é:

(A) 46%.

(B) 48%.

(C) 50%.

(D) 52%.

 

Resolução

Não sabemos a quantidade total de pessoas da festa, mas sabemos que a quantidade é um número múltiplo de 25, pois a cada 25 pessoas, temos 13 moças e 12 rapazes.

Daí, a proporção buscada pode ser representada pela fração:

13/25 = 0,52 = 52%

 

Resposta: D

 

 

18. A prova de um concurso continha 60 questões, e os pontos eram calculados pela fórmula P = 3C – 2E + 120, onde C era a quantidade de questões certas e E a de questões erradas. Um candidato que obteve 225 pontos acertou

(A) 45 questões

(B) 30 questões

(C) 20 questões.

(D) 15 questões.

 

Resolução

Dada a fórmula que calcula a quantidade de pontos, e sabendo que o candidato fez 225, temos:

3C – 2E + 120 = 225

3C – 2E = 225 – 120

3C – 2E = 105

 

Temos outro dado importante, como a prova tem 60 questões, temos que:

C + E = 60
Basta então resolvermos o sistema de equações do primeiro grau:

3C – 2E = 105

C + E = 60
Multiplicando a segunda equação por 2:

3C – 2E = 105

2C + 2E = 120

 

Somando as equações:

3C – 2E + 2C + 2E = 105 + 120

5C = 225

C = 225/5

C = 45

 

Resposta: A

 

 

19. Sabendo-se que uma pessoa consome aproximadamente 800 metros cúbicos de água por ano e que o planeta dispõe de, no máximo, 9000 quilômetros cúbicos de água para o consumo por ano, pode-se afirmar que a capacidade máxima de habitantes que o planeta suporta, considerando-se apenas a disponibilidade de água para consumo, é aproximadamente:

(A) 11.100.000.000.

(B) 11.150.000.000.

(C) 11.250.000.000.

(D) 11.350.000.000.

 

Resolução

Sabe-se que 1 km³ corresponde a 1.000.000.000 m³, daí 9.000 km³ correspondem a 9.000.000.000.000 m³.

9.000.000.000.000 / 800 = 11.250.000.000

 

Resposta: C

 

 

20. Para encher um recipiente com capacidade de 15 litros, a quantidade mínima de vezes que terei de utilizar uma garrafa de refrigerante com capacidade para 600 ml é:

(A) 20.

(B) 25.

(C) 30.

(D) 35.

 

Resolução

Sabe-se que 600ml corresponde a 0,6 litros.

15 / 0,6 = 25

 

Resposta: B

 

 

21.O trabalho realizado por três máquinas durante 6 horas por dia, em 2 dias, custa R$ 1.800,00. Se uma máquina apresentar defeito e parar de funcionar, o custo da operação por 4 dias, com um  funcionamento de 5 horas por dia, é igual a

(A) R$ 1.850,00.

(B) R$ 1.900,00.

(C) R$ 1.950,00.

(D) R$ 2.000,00.

 

Resolução

Vamos resolver a questão utilizando a regra de três composta, onde temos as variáveis “número de máquinas”, “h/d”, “dias” e “custo”.  Repare que as todas as setas estão para cima pois qualquer das grandezas é diretamente proporcional a grandeza “custo”.

 

Máquinas      h/d      dias      custo

3                      6          2           1800

2                      5          4            x

↑                      ↑          ↑            ↑

 

 

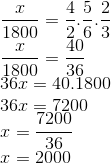
Resposta: D

 

 

Para responder as questões 22 e 23, leia atentamente o texto abaixo. Considere pi aproximadamente igual a 3.

“Para realizar o Teste de Aptidão Física (TAF), as Forças Armadas utilizam uma pista cujas laterais são semelhantes a um retângulo com a largura igual à metade do comprimento, tendo, nas extremidades do comprimento, dois semicírculos.”

Analisando as informações acima, podemos desenhar a pista de corrida. Veja:

 

 

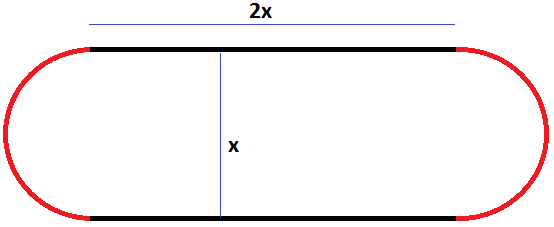
22. Se o comprimento da pista é igual a 420 m, entã o raio dos semicírculos é igual a

(A) 30 m.

(B) 35 m.

(C) 40 m.

(D) 45 m.

 

Resolução

O comprimento da pista nada mais é do que o perímetro da figura, formada por duas retas de comprimento 2x e um círculo de raio x/2. Temos então:

2x + 2x + 2πx/2 = 420

4x + πx = 420

 

Como devemos considerar π=3:

4x + 3.x = 420

4x + 3x = 420

7x = 420

x = 420/7

x = 60

 

Como x é o dobro do raio, temos que o raio dos semicírculos é 30 metros.

 

 

23. A área, em metros quadrados, ocupada pela pista é igual a

(A) 6900.

(B) 7900.

(C) 8900.

(D) 9900.

 

Resolução

A área total será a área do retângulo somada a área da circunferência:

Ar = 2x.x = 2x² = 2.60² = 2.3600 = 7200

Ac = π.r² = 3.30² = 3.900 = 2700

At = 7200 + 2700 = 9900 m²

 

Resposta: D

 

 

24. Nos Jogos da Polícia Militar, a delegação de um batalhão obteve 37 medalhas. Sendo o número de medalhas de prata 20% superior ao das de ouro, e o número de medalhas de bronze 25% superior ao das de prata, o número de medalhas de prata obtido por essa delegação foi de

(A) 17.

(B) 15.

(C) 12.

(D) 10.

 

Resolução

Sejam:

x = número de medalhas de ouro

y = número de medalhas de prata

z = número de medalhas de bronze

 

Pelas informações da questão temos:

x + y + z = 37

y = 1,2.x

z = 1,25.y

 

Substituindo as equações 2 e 3 na primeira, de modo que tenhamos apenas a incógnita y:

x + y + z = 37

y/1,2 + y + 1,25.y = 37

 

Multiplicando tudo por 1,2:

y/1,2 + y + 1,25.y = 37

y + 1,2y + 1,2.1,25.y = 1,2.37

y + 1,2y + 1,5.y = 44,4

3,7y = 44,4

y = 44,4/3,7

y = 12

 

 

Resposta: C

 

 

25. Ao se aumentar em 2 m um dos lados de uma sala de forma quadrangular, e o outro lado em 3 m, a sala tornou-se retangular, com 56 m² de área. Então, a medida, em metros, do lado do quadrado era igual a

(A) 5.

(B) 6.

(C) 7.

(D) 8.

 

Resolução

Como a sala era quadrada, vamos considerar que os lados mediam x.

Como um lado aumentou em 2 metros e o outro aumentou em 3 metros, cada lado passou a ser de x+2 e x+3.

 

Sabendo que a nova sala tem área igual a 56 m²:

(x + 2).(x + 3) = 56

x² + 3x + 2x + 6 – 56 = 0

x² + 5x – 50 = 0

 

Temos uma equação do segundo grau, que vamos resolver pelo método da soma e produto:

S = -b/a = -5/1 = -5

P = c/a = -50/1 = -50

 

Os dois números cuja soma é -5 e o produto é -50 são -10 e 5.

Como x representa uma medida, descartamos o -10 e temos que cada lado da sala antiga media 5 metros.

 

Resposta: A

 

 

26. Uma praça tem a forma de um triângulo ABC, retângulo em A, cuja hipotenusa a mede 250 metros e o cateto c mede 200 metros. Para garantir a execução de um serviço, houve necessidade de se interditar uma parte da praça com uma corda MN perpendicular à hipotenusa, distando 150 metros do vértice B, com M na hipotenusa e N no cateto c. O comprimento dessa corda, em metros, é

(A) 112,5.

(B) 125,5.

(C) 150,5.

(D) 175,5.

 

Resolução

Com as informações do enunciado, o formato da praça pode ser representado pela figura abaixo:

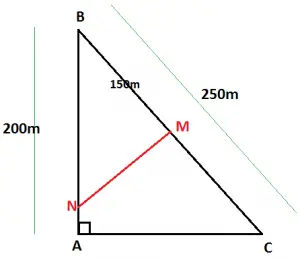
Nosso primeiro passo é acharmos o valor de AC através do teorema de Pitágoras:

BC² = AB² + AC²

250² = 200² + AC²

62500 = 40000 + AC²

AC² = 62500 – 40000

AC² = 22500

AC = 150

 

Pela semelhança dos triângulos ABC e MBN:

 

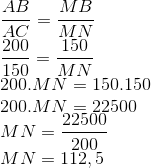
Resposta: A

 

 

27. Dois amigos dividiram uma conta de R$ 135,00. O mais velho apresentou certa quantia e o mais novo completou com dois terços da quantia apresentada pelo mais velho. O valor que o mais novo apresentou foi igual a

(A) R$ 84,00.

(B) R$ 74,00.

(C) R$ 64,00.

(D) R$ 54,00.

 

Resolução

Seja x o valor pago pelo mais velho. Temos

x + 2x/3 = 135

3x + 2x = 405

5x = 405

x = 405/5

x = 81

 

Logo, o mais novo pagou:

135 – 81 = 54

 

Reposta: D

 

 

28. Uma pessoa, após receber seu salário, gasta um quinto com transporte e, do que sobra, gasta um terço com alimentação, restando-lhe ainda R$ 480,00. Seu salário é

(A) R$ 810,00.

(B) R$ 840,00.

(C) R$ 870,00.

(D) R$ 900,00.

 

Resolução

Sendo x o salário dessa pessoa, o que sobra após gastar 1/5 com transporte é 4x/5.

Após gastar com transporte, a pessoa gasta 1/3 do que sobra com alimentação, restando-lhe 2/3, que é igual a 480 reais. Temos

(4x/5).(2/3) = 480

8x/15 = 480

8x = 480.15

8x = 7200

x = 7200/8

x = 900

 

Resposta: D

 

 

29. Para se obter um saldo de R$ 20.000,00, aplicando-se um capital de R$ 10.000,00 a 2% ao mês, no sistema de juros simples, são necessários

(A) 3 anos e 1 mês.

(B) 4 anos e 2 meses.

(C) 5 anos e 3 meses.

(D) 6 anos e 4 meses.

 

Resolução

Queremos que um capital de 10 mil renda mais 10 mil de juros.

2% de 10.000,00 é 200,00

No regime de juros simples o rendimento será sempre de 200 reais por mês.

10000 / 200 = 50 meses

50 meses = 4 anos e 2 meses

 

Resposta: B

 

 

30. A soma das idades de duas pessoas é igual a 44 anos, e, quando somamos os quadrados dessas idades, obtemos 1000. A mais velha das duas tem

(A) 19 anos.

(B) 21 anos.

(C) 22 anos.

(D) 26 anos.

 

Resolução:

Sejam x e y as idades das duas pessoas.

Pelo enunciado, temos:

x + y = 44

x² + y² = 1000

 

Pela primeira equação temos y = 44 – x, que substituído na segunda equação:

x² + y² = 1000

x² + (44 – x)² = 1000

x² + 1936 – 88x + x² = 1000

2x² – 88x + 936 = 0

x² – 44x + 468 = 0

 

Vamos achar as raízes da equação do segundo grau através do método da soma e produto:

S = -b/a = 44/1 = 44

P = c/a = 468/1 = 468

 

Os dois números cuja soma é 44 e o produto é 468 são 18 e 26:

18 + 26 = 44

18.26 = 468

A idade da pessoa mais velha é 26.

 

Resposta: D

 

Gostou da prova resolvida da PM do Pará realizada aplicada em 2007 pela Fadesp? Deixe seu comentário e compartilhe nas redes sociais.

Boa sorte a todos!