Apresentamos a prova resolvida e comentada do concurso da Polícia Militar do Espírito Santo realizado pela Funcab em 2013.
41. A Banda Junior da PMES atualmente atende cerca de 250 alunos da rede pública de ensino da Grande Vitória. Desde sua criação, já passaram pela Banda Júnior cerca de 1.000 alunos. O percentual de alunos, atualmente atendidos por esse projeto cultural da PMES, em relação ao total de alunos que já passaram por ele desde a sua criação corresponde a:
A) 15%
B) 20%
C) 25%
D) 30%
E) 35%
Basta efetuarmos a divisão:
250/1000 = 0,25 ou 25%
42. O RPMont, Regimento de Polícia Montada da Polícia Militar, vem prestando sessões de equoterapia à comunidade capixaba. Supondo que 15 profissionais capacitados atendam aos atuais 50 praticantes de equoterapia, o número de novos profissionais que deveriam ser capacitados para que fossem atendidos 30 novos praticantes, seria de:
A) 5
B) 7
C) 8
D) 9
E) 10
Utilizando regra de três:
Pofissionais Praticantes
15 —————— 50
x ——————- 30
50x = 15.30
x = 450/50
x = 9
43. O Batalhão de Polícia Militar Ambiental da PMES contava com um efetivo de 30 policiais em 1987. Em 2012, contava com um efetivo de 180 policiais. Supondo linear a taxa de crescimento do efetivo de policiais no Batalhão de Polícia Militar Ambiental nos últimos 25 anos, e que a mesma taxa de crescimento permanecerá constante nos próximos cinco anos, o número total de policiais no Batalhão de Polícia Militar Ambiental, ao final desses cinco anos, será de:
A) 200
B) 210
C) 220
D) 230
E) 240
Note que o efetivo teve um aumento de 150 policiais em 25 anos, ou seja, 150/25 = 6 por ano.
Logo, nos próximos 5 anos irá aumentar em 30 policiais. 180 + 30 = 210
44. “Em 2011, O Batalhão de Polícia de Trânsito da PMES confeccionou 4.230 autos de infração contra condutores de veículos de carga.Amulta referente ao descumprimento das proibições de tráfego em determinados horários e locais é de natureza média (4 pontos e R$ 85,13 de multa), e está prevista no art. 187 I do Código de Trânsito Brasileiro (CTB).”
O valor total arrecadado, em reais, em decorrência das multas aplicadas, segundo o texto, foi de:
A) R$ 326.999,90
B) R$ 329.000,90
C) R$ 340.099,90
D) R$ 350.990,90
E) R$ 360.099,90

45. A tabela abaixo representa os dados dos balanços das operações do Batalhão de Polícia de Trânsito (BPTran) da Polícia Militar – ES em três grandes feriados nacionais do ano de 2012.
Dia do trabalho: 220 acidentes, 2 mortos, 78 feridos
Dia de finados: 186 acidentes, 2 mortos, 54 feridos
Dia do trabalho: 219 acidentes, 1 mortos, 51 feridos
O valor que melhor representa a média do número de feridos, de acordo com a tabela acima, é:
A) 57
B) 59
C) 61
D) 63
E) 65
(78 + 54 + 51)/3 = 183/3 = 61
46. Com o objetivo de levar orientação e entretenimento, o grupo de Teatro da Polícia Militar do Espírito Santo serve como um elo de aproximação entre a população e a instituição. Ao longo de todos os anos de atuação, o grupo já atraiu um público aproximado de 160 mil pessoas em suas 250 apresentações já realizadas em todo o Espírito Santo. O número médio de pessoas, por apresentação, do Grupo de Teatro da Polícia Militar do Espírito Santo, de acordo com o texto acima, foi de aproximadamente:
A) 640
B) 650
C) 660 160.000/250 = 640
D) 670
E) 680
47. Observe a receita da torta capixaba que é especialmente servida pelos capixabas por ocasião da Semana Santa.
Ingredientes:
– Cebola, alho, azeite doce, azeitona, limão, coentro, cebolinha verde, tomate a gosto
– 500 g de palmito natural previamente cozido
– 200 g de siri desfiado e cozido
– 200 g de caranguejo desfiado e cozido
– 200 g de camarão cozido
– 200 g de ostra cozida
– 200 g de sururu cozido
– 200 g de badejo desfiado e cozido
– 500 g de bacalhau desfiado e cozido
Tabela de preços por kg:
Palmito natural – R$ 20
Siri desfiado – R$ 30
Caranguejo desfiado – R$ 30
Camarão – R$ 40
Ostra – R$ 25
Sururu – R$ 10
Badejo – R$ 35
Bacalhau – R$ 32
O custo total, em reais, com a compra dos camarões e do bacalhau utilizados na receita de uma torta capixaba, de acordo com a tabela, é de, aproximadamente:
A) R$ 40,00
B) R$ 32,00 Camarão: R$ 40 . 0,2 = R$ 8
C) R$ 26,00 Bacalhau: R$ 32 . 0.5 = R$ 16
D) R$ 24,00
E) R$ 16,00 Total: 8 + 16 = 24
48. Polícia Militar apreende mais de 3 kg de pasta base
de cocaína em Linhares Em uma mochila foram apreendidos 84 tabletes plastificados de cocaína e um tablete grande medindo 20 x 10 cm da mesma substância, totalizando cerca de 3 quilos de cocaína, e R$ 91,00 em espécie. Caso o tablete grande mencionado tenha o formato de um paralelepípedo reto retângulo com 6 cm de altura, o valor do volume total de cocaína desse tablete, em cm³, será de:
A) 400
B) 600
C) 800
D) 1.000
E) 1.200
O tablete possui 20 cm de comprimento, 10 cm de largura e 6 cm de altura.
Volume = 20 x 10 x 6 = 1200 cm³
49. Supondo as dimensões internas de cada pino plástico utilizado na embalagem de cocaína como sendo um cilindro de raio 0,5 cm e altura 4 cm, o valor do volume total de cocaína, desse pino plástico, completamente cheio, em cm³, será de:
(Adote o valor aproximado de π = 3 )
A) 2,5
B) 3
C) 3,5
D) 4
E) 4,5
Vamos utilizar a fórmula para calculo de volume do cilindro:
Volume = π . raio² . altura = π.0,5².4 = 3.0,25.4 = 3
50. Desde 8 de janeiro de 2012, o valor da tarifa do transporte coletivo convencional é R$ 2,35 e do transporte seletivo, R$ 2,50. Pedro utiliza diariamente, de segunda a sexta-feira, dois coletivos e dois seletivos para seu transporte. O valor mínimo, em reais, que ele gastará no mês de abril de 2013, com transporte, será:
Dados:
01/04/2013 é segunda-feira
30/04/2013 é terça-feira
A) R$ 213,40
B) R$ 236,30
C) R$ 243,80
D) R$ 251,20
E) R$ 263,10
Gasto diário: 2×2,35 + 2×2,50 = 9,70
9,70 x 22 dias = 213,40
Texto para as questões 51 e 52
Um Batalhão da Polícia Militar de outro Estado concluiu a reforma e ampliação da pista para pousos e decolagens de helicópteros e passou a dotar sua Unidade Militar de uma excelente estrutura física para operar helicópteros. As obras resultaram na ampliação de 256 metros quadrados de pista, elevando a sua área para 400 metros quadrados (20 metros x 20 metros), com área de toque de 13 metros x 13 metros, o que capacita operar com helicópteros com dimensões de até 4 toneladas.
51. Sendo as pistas para pousos e decolagens de helicópteros figuras planas, quadradas, considerando o texto acima, determine, em metros, a medida dos lados dessa pista, anterior à ampliação.
A) 10 m
B) 11 m
C) 12 m
D) 17 m
E) 18 m
Pista anterior: 400 – 256 = 144
Como a pista é quadrada, e raiz de 144 de 12, cada lado mede 12 metros.
52. De acordo com os dados do texto, a diferença entre a área total da pista e a área de toque, após a ampliação, é de, aproximadamente:
A) 213 m²
B) 231 m²
C) 238 m²
D) 251 m²
E) 283 m²
Área total: 400
Área da pista de toque: 13 x 13 = 169
400 – 169 = 231
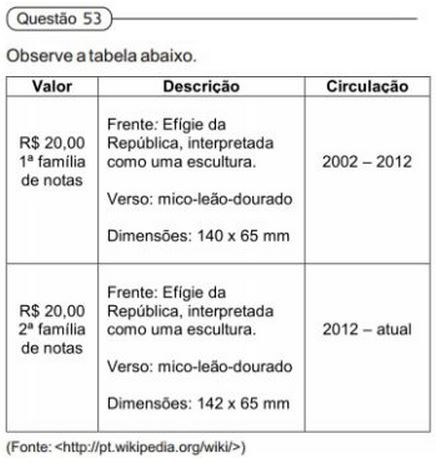
De acordo com os dados da tabela ao lado, o valor da área de papel moeda utilizado a mais para produzir cada nota de R$ 20,00 da segunda família de notas em relação a da primeira família de notas, corresponde, em mm², a:
A) 65
B) 130
C) 150
D) 330
E) 350
A diferença entre as duas notas é de 2 x 65mm = 130mm
54. O subsídio bruto do candidato aprovado neste concurso da Polícia Militar do Estado do Espírito Santo enquanto aluno é de R$ 1.023,32; após incorporação, passa a R$ 2.421,76. Suponha que um candidato aprovado faça um investimento, no sistema de juros simples, de R$ 2.000,00 do seu primeiro salário depois de incorporado, a uma taxa de juros de 5% ao mês, durante 24 meses. O valor total dos juros, em reais, ao final desse período, será de:
A) R$ 2.400,00
B) R$ 2.800,00
C) R$ 3.600,00
D) R$ 4.000,00
E) R$ 4.800,00
Por se tratar de juros simples:
24 x 5% = 120%
120/100 x 2000 = 2400
55. Um policial, pesquisando para comprar seu primeiro imóvel, encontrou o seguinte anúncio:
R$ 100.000,00 – Vende-se apartamento
Apartamento padrão, 2 quartos, 1 banheiro, 60m², sala, cozinha, área de serviço, gesso, ventilador de teto, armário na cozinha, box, sol da manhã.
Valparaiso, Serra-ES
Ele conseguiu um financiamento pelo qual deverá pagar uma entrada correspondente a 10% do valor do imóvel e o restante financiado em 360 parcelas iguais e sem juros.
O valor, em reais, de cada parcela a ser paga por ele será:
A) R$ 175,00
B) R$ 200,00
C) R$ 225,00
D) R$ 250,00
E) R$ 300,00
100.000 – 10% = 90.000
90.000 / 360 = 250
56. Existe um número que somado com seu triplo é igual ao dobro desse número somado com doze.
O valor desse número é:
A) 3
B) 4
C) 5
D) 6
E) 7
Como não sabemos qual é esse número, vamos chamá-lo de x:
x + 3x = 2x + 12
4x = 2x + 12
4x – 2x = 12
2x = 12
x = 12/2
x = 6
57. O conjunto solução da equação x² – 3.x 10 = 0, é:
A) S = {- 5; -1}
B) S = {- 2; 0}
C) S = {- 2; 5}
D) S = {- 2; -5}
E) S = {- 5; 0}
Utilizando o método da soma e produto:
Soma das raízes: -b/a = -(-3)/1 = 3
Produto das raízes = c/a = -10/1 = -10
Veja que:
(-2) + 5 = 3
(-2) . 5 = -10
58. Dada a função quadrática f(x) = 2.x² + 4.x 9, as coordenadas do vértice do gráfico da parábola definida por f(x), é:
A) V = (-7; 1)
B) V = (1; -7)
C) V = (0; 1)
D) V = (-7; 0)
E) V = (0; 0)
Usando a fórmula do x do vértice:
xv = -b/2a = -4/2(-2) = 4/4 = 1
Para calcular o y, basta utilizar x=1:
y = -2.1 + 4.1 – 9 = -2 + 4 – 9 = -7
Clique aqui para assistir a resolução
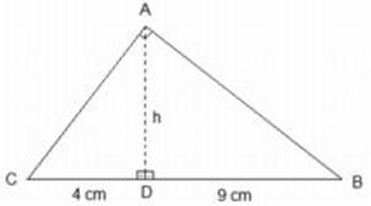
60. A figura abaixo (meramente ilustrativa e fora de escala) representa um triângulo ABC retângulo em A, dividido em dois triângulos, ACD e ABD, ambos retângulos em D.
O valor, em cm, de AD = h, é:
A) 6 cm
B) 7,2 cm
C) 8 cm
D) 8,4 cm
E) 9 cm
61. Sendo a PA= (x; x + 2; 2x 3), o valor de é:
A) 7
B) 8
C) 9
D) 10
E) 11
Vamos descobrir a razão da PA subtraindo a2 – a1:
x + 2 – x = 2
Da mesma forma, a3 – a2 = 2:
2x – 3 – (x + 2) = 2
2x – 3 – x – 2 = 2
x – 5 = 2
x = 7
62. Depois de abertos os portões, o número de pessoas em um evento dobra a cada minuto. Se três pessoas entraram quando os portões foram abertos, o número de pessoas no evento, após os 10 minutos iniciais, será de:
A) 512
B) 1.024
C) 1.536
D) 2.080
E) 3.972
Basta efetuar o cálculo 3x2x2x2x2x2x2x2x2x2x2 = 3072
63. Num churrasco, estima-se que 4 kg de carne são suficientes para satisfazer dez pessoas. Para satisfazermos 120 pessoas, a quantidade mínima de carne, em kg, de acordo com a estimativa anterior, deve ser de:
A) 32 kg
B) 36 kg
C) 40 kg
D) 42 kg
E) 48 kg
Vamos utilizar a regra de três:
Pessoas kg
10 4
120 x
10x = 4.120
10x = 480
x = 480/10 = 48
64. Em um estacionamento, (1/3) dos veículos é automóvel, (1/4) dos veículos é caminhão e os dez veículos restantes são motocicletas. O total de veículos nesse estacionamento é:
A) 18
B) 20
C) 24
D) 28
E) 30
Automóvel + Caminhão:
1/3 + 1/4 = (4 + 3)/12 = 7/12
Logo, 5/12 são motocicletas:
5x/12 = 10
5x = 10.12
5x = 120
x = 120/5 = 24
65. O ano de 2012 terminou com 1.660 pessoas assassinadas no estado do Espírito Santo. Esse número mostra que a redução de homicídios no ano passado foi de x%, em relação a 2011, quando 1.708 pessoas foram mortas. De acordo com o texto, o valor aproximado de é:
A) 1,47
B) 1,79
C) 2,21
D) 2,81
E) 3,18
A redução foi de 1708 – 1660 = 48
48/1708 = 0,0281 = 2,81%
66. João vai dividir um tablete de doce de leite que tem a forma de um paralelepípedo de dimensões 8 x 10 x 6 cm, em cubinhos iguais. O número total de cubinhos de doce de leite, de aresta igual a 2 cm, obtidos por João, depois da divisão, será de:
A) 50
B) 60
C) 70
D) 80
E) 90
O volume dos cubinhos é:
2.2.2 = 8
O volume do tablete é:
8.10.6 = 480
Logo, João vai fazer:
480/8 = 60 cubinhos
67. Um para-raios instalado em um determinado prédio protege uma área circular de raio R = 20 m no solo. O valor total da área do solo, em metros quadrados, protegida por esse para-raios, é de:
(Adote o valor aproximado de π= 3,14)
A) 1.256 m²
B) 1.294 m²
C) 1.306 m²
D) 1.382 m²
E) 1.416 m²
Calculando a área:
Área = pi x raio²
Área = 3,14 x 20²
Área = 3,14 x 400
Área = 1256
Texto para as questões 68, 69 e 70.
Você sabe como se calcula a quantidade de pessoas em uma multidão?
De acordo com engenheiros e estudiosos, o número de pessoas que cabem em 1 m², em um local com grande concentração de pessoas, é de no máximo 7. Isso com as pessoas se espremendo umas nas outras. É mais objetivo levar em consideração um número de 3 a 4 pessoas, mas este número ainda pode variar.
68. Na praia de Copacabana, a área que vai do início da faixa de areia até o calçadão é de aproximadamente 403.500 m². Utilizando uma concentração estimada de sete pessoas por metro quadrado, o número de pessoas que assistiram à tradicional queima de fogos do Reveillon na praia de Copacabana foi de aproximadamente:
A) 2.426.500 pessoas.
B) 2.824.500 pessoas.
C) 2.984.500 pessoas.
D) 3.124.500 pessoas.
E) 3.834.500 pessoas.
403.500 x 7 = 2.824.500
69. Para calcular o número de pessoas que compareceram a um evento, os limites foram estipulados analisando diversas fotos originais feitas por ocasião do evento. Com a ajuda do Google Earth, foi traçada a área total de 2.835 m² que multiplicada pelo número de pessoas, por metro quadrado, estimou-se em aproximadamente 8.505 o número de pessoas presentes, desconsiderando o total de pessoas nos arredores e espalhados fora da área calculada. O número aproximado de pessoas por m², dentro dos limites da área calculada, é de aproximadamente:
A) 2
B) 2,5
C) 3
D) 3,5
E) 4
8.505 / 2.835 = 3
70. Uma festa no pátio de uma escola reuniu um público de 2.800 pessoas numa área retangular de dimensões x e x + 60 metros. O valor de , em metros, de modo que o público tenha sido de, aproximadamente, quatro pessoas por metro quadrado, é:
A) 5 m
B) 6 m
C) 8 m
D) 10 m
E) 12 m
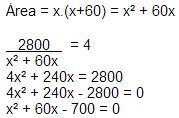
Soma das raízes = -b/a = -60
Produto das raízes: c/a = -700
É fácil observar que as raízes são 10 e -60. Como x representa medida, descartamos o -60