Confira a prova resolvida do concurso para o IBGE realizado em 2016.

As questões foram muito bem elaboradas pela FGV, tanto no conteúdo abordado quanto na complexidade exigida para o cargo.

Bom estudo e boa sorte a todos!

36. As meninas Alice, Beatriz e Celia brincam na balança. Alice e Beatriz juntas pesam 100 kg, Alice e Celia juntas pesam 96 kg e Beatriz e Celia juntas pesam 108 kg. Beatriz pesa:

(A) 48 kg;

(B) 50 kg;

(C) 52 kg;

(D) 54 kg;

(E) 56 kg.

Resolução

Considere:

A = peso da Alice

B = peso da Beatriz

C = peso da Celia

Com as informações apresentadas pela questão, podemos montar 3 equações:

(1) A + B = 100

(2) A + C = 96

(3) B + C = 108

Fazendo (3) – ­(2):

B + C – A – C = 108 – 96

B – A = 12

Vamos agora somar a equação acima com a equação (1):

A + B + B – A = 100 + 12

2B = 112

B = 56

Resposta: E

37. Considere a sequência infinita IBGEGBIBGEGBIBGEG… A 2016ª e a 2017ª letras dessa sequência são, respectivamente:

(A) BG;

(B) GE;

(C) EG;

(D) GB;

(E) BI.

Resolução:

Perceba que a sequência sempre repete as 6 letras IBGEGB.

Como 6 x 336 = 2016, a letra B ocupa a posição 2016 e a letra I ocupa a posição 2017.

Resposta: E

38. A grandeza G é diretamente proporcional à grandeza A e inversamente proporcional à grandeza B. Sabe-­se que quando o valor de A é o dobro do valor de B, o valor de G é 10. Quando A vale 144 e B vale 40, o valor de G é:

(A) 15;

(B) 16;

(C) 18;

(D) 20;

(E) 24.

Resolução:

Como “A grandeza G é diretamente proporcional à grandeza A e inversamente proporcional à grandeza B”, temos que:

G = k.A/B

Neste caso k é a constante de proporcionalidade.

Como “quando o valor de A é o dobro do valor de B, o valor de G é 10”, temos que:

G = k.A/B

10 = k.2

k = 5

Agora que descobrimos o valor de k, vamos achar o valor de G quando A é 144 e B é 40:

G = k.A/B

G = 5.A/B

G = 5.144/40

G = 18

Resposta: C

39. Sobre os números inteiros w, x, y e z, sabe-­se que w>x>2y>3z . Se z=2 , o valor mínimo de w é:

(A) 6;

(B) 7;

(C) 8;

(D) 9;

(E) 10.

Resolução:

Se z=2, temos pelas desigualdades que:

w>x>2y>6

Como w, x, y e z são inteiros, temos que:

y é no mínimo 4, pois aí teríamos w>x>8>6

x é no mínimo 9, pois aí teríamos w>9>8>6

w é no mínimo 10, pois aí teríamos 10>9>8>6

Resposta: E

40. A distância da Terra ao Sol é de 150 milhões de quilômetros e esse valor é chamado de “1 unidade astronômica” (1UA). A estrela Sírius, a mais brilhante do céu, está a 81 trilhões de quilômetros do Sol. A distância de Sírius ao Sol em UA é:

(A) 5.400;

(B) 54.000;

(C) 540.000;

(D) 5.400.000;

(E) 54.000.000.

Resolução:

Basta efetuarmos a seguinte divisão:

81.000.000.000.000 / 150.000.000

Simplificando:

8100000 / 15

2700000 / 5

540000

Resposta: C

41. Um segmento de reta de comprimento C é dividido em cinco partes iguais, e a segunda e a quarta partes são retiradas. A seguir, cada uma das partes restantes é também dividida em cinco partes iguais, e as segundas e as quartas partes são retiradas. A soma dos comprimentos das partes restantes é:

(A) 9C/25

(B) 8C/25

(C) 6C/25

(D) 4C/5

(E) 3C/5

Resolução:

Seja C o comprimento da reta.

Dividindo a reta em 5 partes iguais e retirando duas, restarão:

C.3/5 = 3C/5

Fazendo o processo novamente com os 3 pedaços restantes:

(3C/5).(3/5) = 9C/25

Resposta: A

42. Uma loja de produtos populares anunciou, para a semana seguinte, uma promoção com desconto de 30% em todos os seus itens. Entretanto, no domingo anterior, o dono da loja aumentou em 20% os preços de todos os itens da loja. Na semana seguinte, a loja estará oferecendo um desconto real de:

(A) 10%;

(B) 12%;

(C) 15%;

(D) 16%;

(E) 18%.

Resolução:

Para aumentar o preço em 20%, o comerciante multiplicou cada preço por 1,2.

Para dar o desconto de 30%, o comerciante multiplicou cada preço por 0,7.

Basta agora multiplicarmos esses valores:

1,2 x 0,7 = 0,84

Veja que o desconto real foi de 16%.

Resposta: D

43. Rubens percorreu o trajeto de sua casa até o trabalho com uma determinada velocidade média. Rubinho, filho de Rubens, percorreu o mesmo trajeto com uma velocidade média 60% maior do que a de Rubens. Em relação ao tempo que Rubens levou para percorrer o trajeto, o tempo de Rubinho foi:

(A) 12,5% maior;

(B) 37,5% menor;

(C) 60% menor;

(D) 60% maior;

(E) 62,5% menor.

Resolução:

Considere que o tempo gasto por Rubens foi igual a t, com uma velocidade igual a v.

Precisamos descobrir o tempo gasto por Rubinho, sabendo que sua velocidade foi 60% maior, ou seja 1,6v.

Seja x o tempo gasto por Rubinho.

Utilizando regra de três:

Tempo       Velocidade

t                   v

x                 1,6v

Quanto maior a velocidade, menor o tempo gasto, logo as grandezas são inversamente proporcionais. Temos:

x.1,6v = v.t

x = t/1,6

x = 0,625t

Daí, o tempo gasto por Rubinho é 37,5% menor.

Resposta: B

44. Uma senha de 4 símbolos deve ser feita de forma a conter dois elementos distintos do conjunto {A, B, C, D, E} e dois elementos distintos do conjunto {0, 1, 2, 3, 4, 5}, em qualquer ordem. Por exemplo, a senha 2EC4 é uma das senhas possíveis. Nesse sistema, o número de senhas possíveis é:

(A) 2400;

(B) 3600;

(C) 4000;

(D) 4800;

(E) 6400.

Resolução:

Podemos escolher duas letras entre 5. A quantidade de combinações possíveis será:

5×4 = 20

Podemos escolher dois números entre 6. A quantidade de combinações possíveis será:

6×5 = 30

Agora que já escolhemos as letras e números, temos 6 opções paga formarmos a senha com letras e números. Veja:

LLNN

NNLL

LNLN

LNNL

NLNL

NLLN

A quantidade total de opções será:

20x30x6 = 3600

Resposta: B

45. Quando contamos os números pares em ordem crescente de 1000 até 2500, o número 2016 ocupa a 509ª posição. Quando contamos os números pares em ordem decrescente de 2500 até 1000, o número 2016 ocupa a posição:

(A) 240;

(B) 241;

(C) 242;

(D) 243;

(E) 244.

Resolução:

Vamos então analisar a sequência 2500, 2498, 2496, …, 2016.

Veja que temos uma PA, onde o primeiro termo é 2500, o último termo é 2016 e a razão é ­2.

Vamos utilizar a fórmula do termo geral para descobrimos a quantidade de termos:

an = a1 + (n­1).r

2016 = 2500 + (n­1).(­2)

2016 – 2500 = ­2n + 2

­484 = ­2n + 2

2n = 486

n = 243

Resposta: D

46. O pentágono ABCDE tem área de 125 m2. Esse pentágono foi ampliado a partir do vértice A, como mostra a figura a seguir, transformando­-se no pentágono APQRS cujos lados PQ, QR e RS são, respectivamente, paralelos aos lados BC, CD e DE do pentágono original.

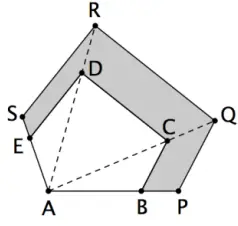
Se AB = 10 m e BP = 2 m , a área da região sombreada na figura é, em m²:

(A) 55;

(B) 64;

(C) 72;

(D) 75;

(E) 80.

Resolução:

Como os polígonos são semelhantes, e considerando x a área do pentágono maior e y a área do pentágono menor, temos que:

x/y = (AP/AB)²

x/125 = (12/10)²

x/125 = 1,22

x/125 = 1,44

x = 1,44.125

x = 180m²

Portanto, a área sombreada é igual a 180 – 125 = 55 m²

Resposta: A

47. Lucas foi a uma feira de jogos levando 45 cartas vermelhas e 45 cartas azuis. Em um quiosque ele pode trocar duas cartas vermelhas por uma carta dourada e uma carta azul. Em outro quiosque ele pode trocar três cartas azuis por uma carta dourada e uma carta vermelha. Lucas fez todas as trocas possíveis para conseguir o máximo de cartas douradas. O número de cartas douradas que Lucas conseguiu com as trocas foi:

(A) 59;

(B) 60;

(C) 61;

(D) 62;

(E) 63.

Resolução:

Lucas tem 45 cartas vermelhas e 45 cartas azuis, vai no segundo quiosque e troca as 45 azuis por 15 douradas e 15 vermelhas.

Resultado: 60 vermelhas e 15 douradas.

Lucas vai no primeiro quiosque e troca as 60 vermelhas por 30 douradas e 30 azuis.

Resultado: 45 douradas e 30 azuis.

Lucas vai novamente no segundo quiosque e troca as 30 azuis por 10 douradas e 10 vermelhas.

Resultado: 55 douradas e 10 vermelhas.

Lucas vai novamente ao primeiro quiosque e troca as 10 vermelhas por 5 douradas e 5 azuis.

Resultado: 60 douradas e 5 azuis.

Lucas vai novamente ao segundo quiosque e troca 3 azuis por uma dourada e uma vermelha.

Resultado: 61 douradas, 2 azuis e 1 vermelha.

Resposta: C

48.Uma pirâmide regular é construída com um quadrado de 6 m de lado e quatro triângulos iguais ao da figura abaixo.

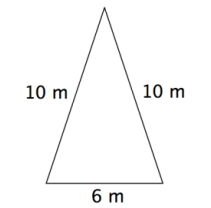
O volume dessa pirâmide em m³ é aproximadamente:

(A) 84;

(B) 90;

(C) 96;

(D) 108;

(E) 144.

Resolução:

Veja que teremos uma pirâmide onde a base é um quadrado de lado 6, e as outras 4 faces são iguais ao triângulo apresentado na figura.

Para calcularmos o volume, precisamos da área da base (6.6 = 36) e a altura da pirâmide.

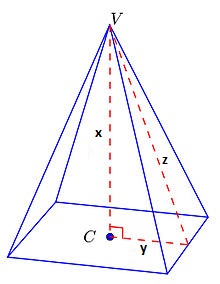
Veja na figura que nosso objetivo então será descobrir o valor de x (altura). Para tanto, precisamos saber os valores de y e z.

y é a metade do lado do quadrado, logo y=3.

z pode ser calculado utilizando o Teorema de Pitágoras no triângulo:

10² = z² + 3²

100 = z² + 9

z² = 91

z = √91

Calculando a altura x:

z² = x² + y²

(√91)² = x² + 3²

91 = x² + 9

x² = 82

x = √82 ≅ 9

Calculando o volume da pirâmide:

V = área da base x altura x 1/3

V ≅ 36.9/3

V ≅ 108

Resposta: D

49. Cinco pessoas estão sentadas em cinco cadeiras em linha, cada uma com uma moeda na mão. As moedas são todas bem equilibradas, de modo que a probabilidade de sair cara ou coroa em cada uma delas é 1/2. Em um determinado momento, as cinco pessoas jogam suas respectivas moedas. Aquelas que obtiverem cara continuam sentadas, e as que obtiverem coroa levantam-­se. Após esse procedimento, a probabilidade de que NÃO haja duas pessoas adjacentes, ambas sentadas ou ambas de pé, é de:

(A) 1/2

(B) 1/8

(C) 1/16

(D) 3/32

(E) 5/32

Resolução:

Temos uma fileira com 5 pessoas. Precisamos que exista uma alternância entre cara e coroa. O resultado do primeiro da fila é irrelevante. Tanto faz se sair cara ou coroa. O que importa é o segundo, que precisa tirar o contrário do primeiro, da mesma forma o terceiro, que precisa tirar o contrário do segundo, …

A probabilidade será:

(1/2) x (1/2) x (1/2) x (1/2) = 1/16

Resposta: C

50. Duas grandezas positivas X e Y são tais que, quando a primeira diminui de 1 unidade, a segunda aumenta de 2 unidades. Os valores iniciais dessas grandezas são X =50 e Y =36. O valor máximo do produto P = XY é:

(A) 2312;

(B) 2264;

(C) 2216;

(D) 2180;

(E) 2124.

Resolução:

Vamos considerar o produto P = (50­n).(36+2n), pois quando diminuímos n vezes 1 de X, aumentamos n vezes o 2 de Y.

P = (50­n).(36+2n)

P = 1800 + 100n – 36n – 2n²

P = – 2n² + 64n + 1800

Temos uma função quadrática com a = -2, b = 64 e c = 1800.

O valor máximo ocorre quando n = -b/2a = -64/2(-2) = 16.

Substituindo n por 16, encontramos o valor máximo de P.

P = (50 – 16)(36+2.16) = 34.68 = 2.312.

Resposta: A

Gostou da prova resolvida do concurso para técnico do IBGE (2016)?

Deixe o seu comentário.