Dando continuidade ao estudo da trigonometria, nesta página iremos abordar a lei do cosseno, ferramenta extremamente útil quando estamos trabalhando com triângulos não retângulos.
É muito importante que o aluno tenha um conhecimento razoável sobre triângulos e razões trigonométricas.
Bom estudo a todos!
A lei do cosseno relaciona medidas de lados e medidas de ângulos em um triângulo não retângulo, onde não podemos utilizar, por exemplo, o Teorema de Pitágoras ou as razões trigonométricas.
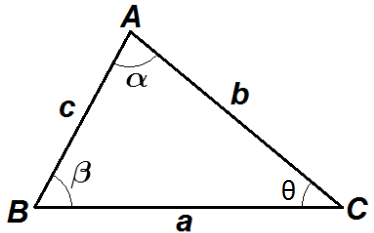
Dado um triângulo ABC qualquer, de ângulos internos α, β, θ, e cujos lados medem a, b e c. Veja a figura:
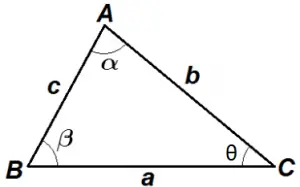
Pela lei dos cossenos, valem as seguintes relações:
a² = b² + c² – 2.b.c.cosα
b² = a² + c² – 2.a.c.cosβ
c² = a² + b² – 2.a.b.cosθ
VAMOS PRATICAR?
Agora que já aprendemos a definição, vamos resolver alguns exemplos.
Exemplo 1. Calcular o cosseno do ângulo x, representado no triângulo abaixo:
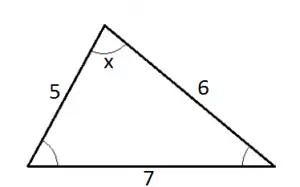
Utilizando a lei do cosseno:
a² = b² + c² – 2.b.c.cosθ
7² = 5² + 6² – 2.5.6.cosx
49 = 25 + 36 – 60.cosx
49 = 61 – 60.cosx
60.cosx = 61 – 49
60.cosx = 12
cosx = 12/60
cosx = 1/5
Exemplo 2: Dado um triângulo ABC, calcule a medida de BC, sabendo que AB = 8, AC = 3 e  = 60°.
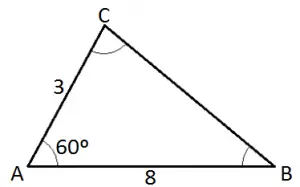
Utilizando a lei do cosseno:
a² = b² + c² – 2.b.c.cosθ
BC² = 8² + 3² – 2.8.3.cos60°
BC² = 64 + 9 – 48.1/2
BC² = 73 – 24
BC² = 49
BC = √49
BC = 7
Exemplo 3: Calcular o valor de k na figura abaixo:
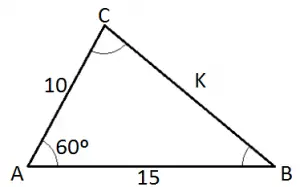
Utilizando a lei do cosseno:
a² = b² + c² – 2.b.c.cosθ
k² = 10² + 15² – 2.10.15.cos60°
k² = 100 + 225 – 300.1/2
k² = 325 – 150
k² = 175
k = √175
k = 5√7