Estudando matemática e raciocínio lógico para concursos? Confira aqui a prova resolvida do concurso para o TJ SP, cargo de escrevente, realizado em 2014 pela Vunesp.
Veja em nosso menu outras provas resolvidas de concursos de tribunais, e também da banca Vunesp.
Bom estudo!
Questão 29. Certa empresa produz diariamente quantidades iguais do produto P. Se essa empresa usar três medidas iguais do componente A em cada unidade do produto final P, serão necessárias 480 dessas medidas para suprir a produção de P durante 2 dias. Se passar a usar 2,5 medidas de A em cada unidade de P, o número de medidas de A necessário para suprir a produção de P, durante 5 dias, será igual a
(A) 1000.
(B) 1050.
(C) 1140.
(D) 1220.
(E) 980.
Resolução
Para resolvermos a questão, devemos calcular a quantidade diária do produto P.
Como são necessários 480 medidas do componente A para fabricar o produto P por dois dias, então são necessárias 240 medidas diárias de A.
Se 3 medidas de A produz um produto P, então a quantidade diária de P é 240/3 = 80 produtos P por dia.
Passando para a segunda parte da questão:
Em 5 dias, serão produzidos 5.80 = 400 produtos P.
Se o número de medidas de A passou para 2,5, basta multiplicarmos:
2,5 x 400 = 1000 medidas de A.
Resposta: A
Questão 30. Um grupo de pessoas participou da fase final de um concurso, sendo que, nesse grupo, o número de mulheres era igual a 3/5 do número de homens. Sabe-se que, concluída a fase final, apenas 1/5 do número de homens e 1/3 do número mulheres foram aprovados, num total de 8 pessoas.
O número de mulheres no grupo que iniciou a participação na fase final desse concurso era igual a
(A) 15.
(B) 12.
(C) 21.
(D) 9.
(E) 18.
Resolução
Seja H a quantidade de homens e H.3/5 a quantidade de mulheres.
Pelo enunciado “1/5 do número de homens e 1/3 do número mulheres foram aprovados, num total de 8 pessoas”, temos a seguinte equação:
(H).1/5 + H.(3/5).(1/3) = 8
H/5 + H/5 = 8
2H/5 = 8
2H = 5.8
H = 40/2
H = 20
Calculando a quantidade de mulheres:
Mulheres = H.3/5 = 20.3/5 = 12
Resposta: B
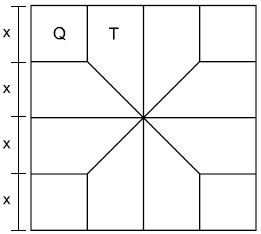
Questão 31. Para efeito decorativo, um arquiteto dividiu o piso de um salão quadrado em 8 regiões com o formato de trapézios retângulos congruentes (T), e 4 regiões quadradas congruentes (Q), conforme mostra a figura:
Se a área de cada região com a forma de trapézio retângulo é igual a 24 m², então a área total desse piso é, em m², igual a
(A) 225.
(B) 196.
(C) 324.
(D) 400.
(E) 256.
Resolução
A informação de que os trapézios e os quadrados são congruentes é muito importante. Dela tiramos que que a região pode ser dividida em 16 quadrados Q, todos de área x².
Sabemos que a área de cada trapézio é 24m². Também não é difícil verificar, observando as congruências, que a área de cada trapézio é 3/2 da área de cada quadrado. Temos então que a área de cada quadrado é 24.(2/3) = 16m².
Como são 16 quadrados, a área total é:
16.16 = 256m²
Resposta: E
Questão 32. Norberto tomou dois empréstimos, que foram pagos após 2 meses com o acréscimo de juro simples. No primeiro, de certo valor, a taxa de juros foi de 1% ao mês. No segundo, de valor R$ 1.600,00 maior que o do primeiro, a taxa de juros foi de 1,5% ao mês. Sabendo que a soma dos juros pagos nos dois empréstimos foi igual a R$ 128,00, é correto afirmar que a soma dos valores desses dois empréstimos é igual a
(A) R$ 3.600,00.
(B) R$ 4.600,00.
(C) R$ 4.800,00.
(D) R$ 3.200,00.
(E) R$ 4.000,00.
Resolução
Considerando:
Primeiro empréstimo:
Valor x; juros simples de 1% a.m.; prazo de 2 meses;
Segundo empréstimo:
Valor (x + 1600), juros simples de 1,5% a.m.; prazo de 2 meses;
Lembrando que nos juros simples, não existem os chamados “juros sobre juros”, vamos calcular os juros pagos:
Primeiro empréstimo:
x.0,01.2 = 0,02.x
Segundo empréstimo:
(x + 1600).0,015.2 = (x + 1600).0,03 = 0,03x + 1600.0,03 = 0,03x + 48
Como os juros totais foram de 128, podemos montar a seguinte equação:
0,02.x + 0,03x + 48 = 128
0,05x = 128 – 48
0,05x = 80
x = 80/0,05
x = 1600
Concluímos então que o primeiro empréstimo foi de 1600 e o segundo de 3200.
Daí, o total foi de 4800.
Resposta: C
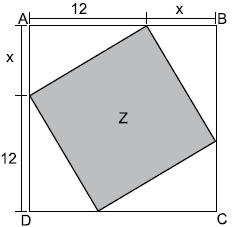
Questão 33. Em uma folha quadrada ABCD, foi desenhado um quadrado Z, de área igual a 169 cm², conforme mostra a figura:
Nessas condições, é correto afirmar que o perímetro da folha ABCD, em centímetros, é igual a
(A) 60.
(B) 56.
(C) 72.
(D) 68.
(E) 64.
Resolução
Como a área do quadrado Z foi dada, podemos descobrir quanto mede cada lado (L), basta calcularmos a raiz quadrada de 169:
L = √169 = 13
Agora que calculamos o lado do quadrado Z, podemos calcular o valor de x, observando que o triângulo na figura de lados x, 12 e L é retângulo, onde podemos aplicar o teorema de pitágoras.
Considerando L a hipotenusa, temos:
L² = 12² + x²
13² = 12² + x²
169 = 144 + x²
x² = 169 – 144
x² = 25
x = √25
x = 5
Assim, temos que cada lado de ABCD mede 12 + 5 = 17cm, e o perímetro é de 4.17 = 68cm
Resposta: D
Questão 34. Considere um reservatório com o formato de um paralelepípedo reto retângulo, com 2 m de comprimento e 1,5 m de largura, inicialmente vazio. A válvula de entrada de água no reservatório foi aberta por certo período, e, assim, a altura do nível da água no reservatório atingiu 50 cm, preenchendo 40% da sua capacidade total. Desse modo, é correto afirmar que a medida da altura desse reservatório, em metros, é
igual a
(A) 1,35.
(B) 1,25.
(C) 1,50.
(D) 1,75.
(E) 1,65.
Resolução
Como trata-se de um reservatório no formato de um paralelepípedo reto retângulo, a capacidade é diretamente proporcional a altura deste, tornando nesta questão, as informações sobre comprimento e largura irrelevantes.
Considerando a altura igual a h temos:
40% de h = 50 cm
0,4.h = 50
h = 50/0,4
h = 125 cm ou 1,25 m
Resposta: B
Questão 35. A Câmara dos Deputados aprovou ontem a Medida Provisória n. 647, que permite ao governo elevar para até 27,5% o limite de etanol anidro misturado à gasolina vendida nos postos de combustível. Hoje, esse teto é de 25%.
(O Estado de S.Paulo, 07.08.2014)
Suponha que dois tanques, A e B, contenham quantidades iguais, em litros, de um combustível formado pela mistura de gasolina e de álcool anidro, sendo 25% o teor de álcool na mistura do tanque A e 27,5%, o teor de álcool na mistura do tanque B. Nessas condições, é correto afirmar que a quantidade de álcool no tanque B supera a quantidade de álcool no tanque A em
(A) 2,5%
(B) 7,5%
(C) 10%
(D) 8%
(E) 5%
Resolução
Nota-se que, sobre o combustível, a diferença entre as quantidades de álcool é de 2,5%, pois em um tanque o álcool representa 25% e em outro representa 27,5%.
Precisamos apenas calcular quanto 2,5 representa sobre 25, que é claramente 10%.
Resposta: C
Questão 36. Um feirante compra mangas ao preço de R$ 0,80 para cada duas unidades. Certo dia, ele vendeu 120 mangas ao preço de R$ 6,60 para cada 6 unidades e n mangas ao preço de R$ 4,50 para cada 5 unidades. Se, nesse dia, o lucro obtido com a venda das mangas foi igual a R$ 224,00, então o número total de mangas que o feirante vendeu, nesse dia, foi
(A) 400.
(B) 320.
(C) 480.
(D) 280.
(E) 420.
Resolução
Como ele compra duas mangas por 0,80, cada manga é comprada por 0,40.
Ao vender 120 mangas ao preço de 6,60 o pacote com 6, é fácil verificar que ele vendeu 20 pacotes. Daí:
Faturamento = 20.6,60 = 132,00
Custo = 120.0,4 = 48,00
Lucro = 132 – 48 = 84,00
Da mesma forma, ao vender n mangas ao preço de 4,50 o pacote com 5, temos que ele vendeu n/5 pacotes. Daí:
Faturamento = (n/5).4,50 = 0,90.n
Custo = 0,40.n
Lucro = 0,90.n – 0,40.n = 0,50.n
Como o lucro nesse dia foi de 224,00, temos:
84 + 0,50.n = 224
0,50.n = 224 – 84
0,50.n = 140
n = 140/0,5
n = 280 mangas
Total de mangas: 120 + 280 = 400 mangas
Resposta: A
Questão 37. Certa competição tem 6 etapas eliminatórias. Sabe-se que a média aritmética do número de pessoas que participaram da primeira e da segunda etapa é igual ao quádruplo da média aritmética do número de pessoas que participaram de cada uma das quatro etapas seguintes. Desse modo, a razão entre o número de pessoas que participaram da primeira e da segunda etapa e o número total de pessoas que participaram dessa competição é de
a) 1/2
b) 1/3
c) 1/4
d) 2/3
e) 3/4
Resolução
Vamos representar cada etapa pelas letras a, b, c, d, e, f, nesta ordem.
Temos pelo enunciado:
(a + b)/2 = 4.(c + d + e + f)/4
(a + b)/2 = (c + d + e + f)
Somando (a + b) em ambos os lados temos:
(a + b)/2 + (a + b) = (c + d + e + f) + (a + b)
(a + b)/2 + 2(a + b)/2 = (a + b + c + d + e + f)
(a + b)3/2 = (a + b + c + d + e + f)
(a + b) = (a + b + c + d + e + f)2/3
Logo, a quantidade de participantes das duas primeiras etapas representa 2/3 do total.
Resposta: D
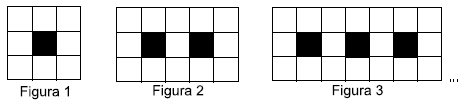
Questão 38. Observe a sequência de figuras feitas em uma malha quadriculada, sendo cada figura composta por quadradinhos brancos e pretos.
De acordo com a lei de formação dessa sequência, o número de quadradinhos brancos na figura 18 será igual a
(A) 103.
(B) 108.
(C) 113.
(D) 98.
(E) 93.
Resolução
A quantidade total de quadradinhos é:
Figura1: 3.3 = 9
Figura2: 3.5 = 15
Figura3: 3.7 = 21
Figura4: 3.9 = 27
…
Temos na verdade uma PA onde a1 = 9 e a razão é 6. Vamos calcular o a18:
Pela fórmula do termo geral da PA:
an = a1 + (n – 1).r
a18 = 9 + (18 – 1).6
a18 = 9 + 17.6
a18 = 9 + 102
a18 = 111
Descontando os 18 quadradinhos pretos da figura 18, temos 111 – 18 = 93
Resposta: E
Clique aqui para acessar a página 2, onde encontram-se as questões sobre raciocínio lógico.

Apreciei muito as respostas,porém a questão 29 no Gabarito informa como sendo a resposta correta a letra C – 1140 não a Letra A – 1000 conforme foi corrigida a prova.
Ficou a dúvida nesta questão.
Adriano,
Verifiquei a questão novamente, aparentemente não existe erro.
Confira a versão de sua prova ao comparar com o gabarito.
Caso a dúvida persista, podemos analisar novamente, e se necessário, formularmos um recurso.
Boa sorte.
Por favor,
Tenho uma dúvida na questão 37 e preciso da sua ajuda.
Porque no desenvolvimento do calculo soma (a+b) nos dois lados da equação?
Obrigada.
Olá Kelly,
Somar a+b em ambos os lados não é uma regra, foi um artifício que utilizamos para resolver a questão, onde necessitávamos que em um lado aparecesse a soma a+b+c+d+e+f.
Boa sorte.
Como faço pra saber a versão da minha prova?
Odair,
Não fiz a prova, como o caderno de questões não foi fornecido ao final da prova, penso que se você entrar no site da Vunesp deve conseguir a informação.
Boa sorte!
Valeu, obrigado!
A questão 37. é anulável pelo seguinte motivo
ela pressupõe que qualquer competição com 6 etapas eliminatórias, n1..n6 que atenda apenas à condição de media(n1..n2) = 4x(n3..n6)
terá razão 2/3… Preguiça de examinador é de doer, me fez perder meu tempo de prova 3~4 minutos, pular e chutar por falta de tempo.
Pois bem, são tantas as exceções, e basta mostrar uma, e isso invalida a questão( lembre que logica está no edital e TODO…é nega-se com Algum não é..rs )
Para os que desejarem recorrer, bastaria uma única restrição adicional para manter o gabarito n1+n2+n3+n4+n5+n6=n !!
Existe alguma restrição a ter 2 etapas com números iguais ? não!
Existe alguma restrição que diga, quem não participou da etapa i não pode participar da seguinte ? Não
Existe alguma restrição que diga, todo participante deve participar de todas as eliminatórias? Não…
Bem só aqui tem 4 possibilidades de argumentar, divirtam-se!
Ronaldo,
Verifique que em nossa resposta, consideramos a, b, c, d, e, f, como valores quaisquer, portanto estamos considerando a possibilidade de termos duas etapas com valores iguais. Quanto a segunda e terceira perguntas, existe sim, as etapas são eliminatórias.
Bons estudos!
Na questão 38 o gabarito do site da Vunesp está dando como correta a alternativa D = 98, mas também cheguei a resposta 93. Será que houve erro no gabarito deles?
Olá Mariana,
Conferi e não achei erros na resolução…
Analisando a questão de outra forma, chegamos ao mesmo resultado:
A primeira figura tem 8 quadradinhos brancos.
Repare que sempre aumentamos 5 quadradinhos brancos de uma figura para outra.
A figura 18 terá então 8 + 5.17 = 8 + 85 = 93
Bons sorte!
Conforme gabarito, a resposta da questão 63 é equivalente a alternativa E.
Lorena,
veja o que a letra E afirma:
(E) Luiz pertence ao Partido dos Esforçados.
A afirmação IV diz que “Luiz não é candidato a vereador”, logo ele é candidato a prefeito.
A afirmação V diz que “Nenhum dos filiados do Partido dos Esforçados quis ser candidato à prefeitura”
Veja que se a afirmação E fosse verdadeira, as afirmações IV e V seriam contraditórias.
Na Questão 30, por que multiplicamos H3/5 por 1/3 ao invés de dividir? Qual é a explicação?
Cara Luciana,
multiplicar por 1/3 ou dividir por 3 é exatamente a mesma coisa.
Bons estudos.
Olá Jordon,
Sobre a Questão 38, por quê temos que a razão é 6? Não entendi…
Obrigado
Olá Renato,
A razão refere-se a quantidade de quadradinhos que são acrescentados de uma figura para outra. No caso, sempre são acrescentados 6 quadradinhos.
Continue sempre ajudando com esse excelente trabalho, adorei o seu post.
Você planeja fazer algum outro post sobre esse mesmo assunto?
Já está divulgado e curtido! Muito bom!