Olá amigos concurseiros! Hoje apresentamos a prova resolvida do concurso para Agente de Pesquisa e Mapeamento do IBGE, realizado em 2016 pela Cesgranrio.

A banca foi muito feliz na escolha das questões de raciocínio lógico matemática, exigindo bastante dos candidatos.

Boa sorte a todos!

 

 

46. Considere a seguinte argumentação:

Se alguém tivesse faltado à festa, então todos teriam passado por interesseiros.

No entanto, alguém não passou por interesseiro. Conclui-se que

(A) alguém foi à festa, mas não todos.

(B) não houve festa.

(C) quem faltou à festa é interesseiro.

(D) todos faltaram à festa.

(E) ninguém faltou à festa.

 

Resolução

Podemos resolver a questão apenas sabendo que A→B e sua negação, ~B→~A são equivalentes.

 

Temos que a negação da afirmação: “Se alguém tivesse faltado à festa, então todos teriam passado por interesseiros” é “Se alguém não se passou por interesseiro, então ninguém faltou à festa”.

 

Como a questão afirma que “alguém não passou por interesseiro”, podemos concluir que “ninguém faltou à festa”.

 

Resposta: E

 

 

47. Considere as seguintes definições:

1 – Um triângulo é chamado de escaleno quando os seus lados possuem comprimentos diferentes.

2 – Um triângulo é chamado de isósceles quando há dois de seus lados com o mesmo comprimento.

3 – Um triângulo é chamado de equilátero quando todos os seus lados possuem o mesmo comprimento.

De acordo com as definições apresentadas, um triângulo não é escaleno quando, e apenas quando, ele

(A) é isósceles.

(B) é isósceles, mas não é equilátero.

(C) não é isósceles.

(D) não é equilátero, nem é isósceles.

(E) não é equilátero.

 

Resolução

Conforme definição, um triângulo é escaleno quando todos os lados possuem comprimentos diferentes. Logicamente, um triângulo não é escaleno quando possui pelo menos dois lados iguais, ou seja, quando é isóceles.

Obs: A resposta pode gerar dúvidas pois não mencionamos o equilátero, mas não está incorreto, pois todo triângulo equilátero também é considerado isóceles.

 

Resposta: A

 

 

48. O setor de uma empresa enviou os seus 10 funcionários para participarem de um curso sobre a utilização de um sistema de preenchimento de relatórios. Ao final do curso, todos os funcionários passaram a utilizar o sistema no mesmo ritmo, isto é, cada um passou a preencher a mesma quantidade de relatórios por hora: cada 4 funcionários preenchem 48 relatórios em 6 horas.

Após o curso, em quantas horas 8 funcionários preencheriam 96 relatórios?

(A) 3

(B) 12

(C) 4

(D) 8

(E) 6

 

Resolução

A questão pode ser resolvida apenas observando que a quantidade de funcionários dobra (4 para 8), a medida que a quantidade de relatórios também dobra (48 para 96), ou seja, não é necessário aumentar ou diminuir a quantidade de horas.

A outra opção seria resolver através da regra de três composta. Vamos montar e deixar a cargo do aluno:

Funcionários       Relatórios        Horas

4                             48                      6

8                             96                      x

 

Resposta: E

 

 

49. Maria disse que sua família possui um único carro. Se Maria mentiu, então a sua família

(A) não possui carro, ou possui mais de um carro.

(B) não possui carro.

(C) possui outro tipo de veículo.

(D) não gosta de carros.

(E) possui mais de um carro.

 

Resolução

Negar que Maria tem um único carro é dizer que ou ela não tem, ou ela possui dois ou mais carros.

 

Resposta: A

 

 

50. Cinco amigos passaram o final de semana juntos em uma pousada. O valor total da conta foi de R$ 3.720,40, e cada um pagou apenas a parte que lhe cabia, dentre as despesas de hospedagem, passeios e frigobar.

É necessariamente verdade que

(A) algum amigo gastou mais do que R$ 744,05.

(B) cada amigo gastou mais do que R$ 740,05.

(C) algum amigo gastou menos do que R$ 744,00.

(D) cada amigo gastou menos do que R$ 745,00.

(E) algum amigo gastou entre R$ 744,00 e R$ 745,00.

 

Resolução

Dividindo o valor total por 5:

3.720,40 / 5 = 744,08

Podemos então concluir que, caso a conta tenha sido dividida em partes iguais, cada um pagou 744,08. De onde podemos concluir que pelo menos algum amigo gastou mais do que 744,05.

 

Resposta: A

 

 

51. Todos os funcionários de uma empresa encerram suas atividades às 18h e seguem para suas casas usando ônibus ou van. Os funcionários que usam ônibus seguem até a rodoviária e lá pegam outro ônibus ou um táxi. Os funcionários que usam a van seguem até a zona portuária e lá pegam as barcas.

Portanto, os funcionários que não usam táxi para seguirem para suas casas, após encerrarem suas atividades,

(A) não usam ônibus.

(B) usam ônibus, se não usarem a barca.

(C) não usam barca, mas usam van.

(D) usam ônibus, mas não usam a barca.

(E) não usam van, se usarem a barca.

 

Resolução

Os funcionários saem da empresa através de ônibus ou van.

Os que saem de ônibus seguem para a rodoviária e lá pegam ônibus ou táxi.

Os que saem de van pegam barcas.

 

Queremos analisar os que não usam táxi.

Na primeira opção seriam os que pegam dois ônibus.

Na segunda opção seria van e barcas.

Veja que ou o funcionário usa barca ou ônibus.

 

Resposta: B

 

 

52. A Figura mostra as cinco etapas seguidas para se dobrar uma folha de papel, conforme disposta inicialmente na etapa 1. Foram feitas duas dobras, nas etapas 2 e 4, ao longo dos segmentos tracejados, que dividem ao meio a folha presente nas etapas 1 e 3, respectivamente.

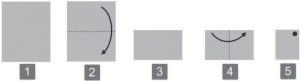
Na etapa 5, no local indicado pelo ponto, a folha dobrada foi atravessada perpendicularmente por um lápis, sendo feito um furo de lado a lado. Se a folha for desdobrada e retornar à forma disposta na etapa 1, então qual a representação correta da disposição dos furos obtidos?

 

Resolução

Esse é o tipo de questão que é possível resolver apenas observando atentamente todos os passos.

Resposta: C

 

 

53. Considere cinco punhados idênticos de feijões, ou seja, com a mesma quantidade de feijão. Tais punhados estão enfileirados e numerados do primeiro ao quinto. Uma pessoa retira de cada punhado, exceto do terceiro, três feijões e os coloca no terceiro punhado. Em seguida, essa pessoa retira do terceiro punhado tantos feijões quantos restaram no segundo e os coloca no primeiro punhado. Após os procedimentos realizados por essa pessoa, quantos feijões sobraram no terceiro punhado?

(A) 7

(B) 15

(C) 9

(D) 12

(E) 10

Resolução

Vamos considerar que cada um dos cinco punhados de feijão contenha uma quantidade x de grãos. Vamos analisar cada uma das etapas.

 

Quando “Uma pessoa retira de cada punhado, exceto do terceiro, três feijões e os coloca no terceiro punhado”,  cada um dos punhados passa a ter x-3 grãos, exceto o terceiro punhado, que recebeu 3 grãos de cada um dos outros 4 e passou a ter x+12.

 

Quando  “essa pessoa retira do terceiro punhado tantos feijões quantos restaram no segundo e os coloca no primeiro punhado”, basta analisarmos que o terceiro tinha x+12 e o segundo tinha x-3. Fazendo a subtração:

= x+12 – (x-3)

= x+12-x+3

= 15

 

Resposta: B

 

 

54. Na Figura a seguir, PQ mede 6 cm, QR mede 12 cm, RS mede 9 cm, e ST mede 4 cm.

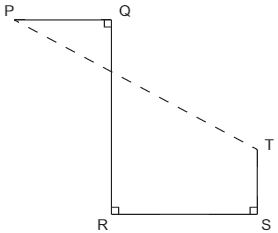
A distância entre os pontos P e T, em cm, mede

(A) 17

(B) 21

(C) 18

(D) 20

(E) 19

 

Resolução

Vamos marcar na figura as distâncias fornecidas e um ponto Z, de modo que tenhamos um triângulo retângulo onde PT é a medida da hipotenusa.

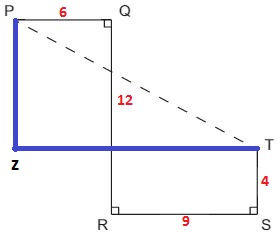
Como temos um triângulo retângulo iremos utilizar o famoso teorema de Pitágoras, onde:

PT = hipotenusa

PZ = 12 – 4 = 8

ZT = 6 + 9 = 15

 

PT² = 8² + 15²

PT² = 64 + 225

PT² = 289

PT = 17

 

Resposta: A

 

 

55. Em cada jogo de um torneio de futebol, um time pode vencer, se fizer mais gols que o adversário, empatar, se fizer o mesmo número de gols que o adversário, ou perder, se fizer menos gols que seu adversário. Um determinado time de futebol jogou três partidas e ficou com saldo de gols positivo, ou seja, fez mais gols do que sofreu.

Qual das campanhas a seguir NÃO pode ter sido a campanha do time citado?

(A) 1 Vitória, 0 Derrota e 2 Empates

(B) 2 Vitórias, 0 Derrota e 1 Empate

(C) 0 Vitória, 1 Derrota e 2 Empates

(D) 1 Vitória, 2 Derrotas e 0 Empate

(E) 1 Vitória, 1 Derrota e 1 Empate

 

Resposta

Analisando as regras do jogo/campeonato, é impossível para um time ficar com saldo positivo no final de 3 partidas sem ganhar pelo menos um jogo.

Resposta: C

 

 

56. A Figura a seguir mostra as flores de um canteiro, e o número abaixo de cada flor  representa a quantidade, em mg, de pólen de cada uma das flores.

Uma abelha visita esse canteiro para colher pólen, mas consegue carregar, no máximo, 8 mg de pólen por viagem. Sabe-se ainda que, em cada viagem, a abelha colhe o pólen de uma única flor, que pode ser revisitada em outras viagens.

Qual a quantidade máxima de pólen, em mg, que essa abelha consegue colher em 24 viagens?

(A) 180

(B) 192

(C) 184

(D) 191

(E) 190

 

Resolução

Repare que a abelha não pode passar em duas flores na mesma viagem e que carrega no máximo 8 mg de pólen. Cada viagem deve ser a mais produtiva possível, ou seja, primeiro ela deve fazer as viagens onde pode carregar 8 mg, e se necessário, buscar outras com menos.

Vamos considerar que ela visita cada flor e só faz viagens onde carrega 8 mg. Após visitar todas, o resultado é o seguinte:

Primeira flor: A abelha não carregou nada e a flor continua com 6 mg.

Segunda flor: A abelha deu 6 viagens, carregando 48 mg, e a flor ficou com 4 mg.

Terceira flor: A abelha deu 4 viagens, carregando 32 mg, e a flor ficou com 3 mg.

Quarta flor: A abelha deu 10 viagens, carregando 80 mg, e a flor ficou com 2 mg.

Quinta flor: A abelha deu 2 viagens, carregando 16 mg, e a flor ficou com 7 mg.

Sexta flor: A abelha deu 1 viagem, carregando 8 mg, e a flor ficou com 3 mg.

 

No total, a abelha chegou a dar 23 viagens, onde carregou 8 mg em cada, ou seja, 184 mg. Agora ela deve dar a última viagem, escolhendo a flor onde tem mais pólen. Podemos verificar que essa flor é a quinta, que possui 7 mg. Logo, a abelha dará 24 viagens carregando:

184 + 7 = 191 mg

 

Resposta: D

 

 

57. Em uma prova de múltipla escolha, todas as questões tinham o mesmo peso, ou seja, a cada questão foi atribuído o mesmo valor. Aldo tirou nota 5 nessa prova, o que corresponde a acertar 50% das questões da prova. Ao conferir suas marcações com o gabarito da prova, Aldo verificou que acertou 13 das 20 primeiras questões, mas constatou que havia acertado apenas 25% das restantes.

Quantas questões tinha a prova?

(A) 24

(B) 84

(C) 32

(D) 72

(E) 52

 

Resolução

Seja x a quantidade restante de questões.

(13 + 25%.x)/(20 + x) = 50%

(13 + 0,25x)/(20 + x) = 0,5

13 + 0,25x = 0,5.(20 + x)

13 + 0,25x = 10 + 0,5x

0,5x – 0,25x = 13 – 10

0,25x = 3

x = 3/0,25

x = 12

 

Total = 20 + 12 = 32

Resposta: C

 

 

58. Antes da final do Novo Basquete Brasil, 9 pessoas foram convidadas a participar de uma apresentação na qual cada uma delas faria 8 arremessos livres à cesta. Dentre essas pessoas havia alguns profissionais, e o restante era composto de torcedores que foram escolhidos aleatoriamente.

Os números de arremessos convertidos pelos participantes foram: 1, 2, 2, 3, 4, 5, 5, 6 e 7. Nenhum torcedor acertou mais arremessos do que qualquer um dos profissionais. Apenas 2 torcedores converteram o mesmo número de arremessos, e um torcedor converteu o mesmo número de arremessos que um profissional.

Quantos profissionais foram convidados para a apresentação?

(A) 7

(B) 3

(C) 6

(D) 4

(E) 5

 

Resolução

Os nenhum torcedor foi melhor que um profissional.

Somente dois torcedores acertaram a mesma quantidade de arremessos, de onde podemos concluir que cada um acertou 2 arremessos.

Como um torcedor empatou com um profissional, a única opção que temos é que cada um acertou 5 arremessos.

De onde concluímos que existiam 3 profissionais.

 

Resposta: B

 

 

59. Ao duplicar a largura de um determinado retângulo e reduzir à metade o comprimento desse mesmo retângulo, obtém-se um quadrado de perímetro P.

O perímetro do retângulo original é

(A) 2,5P

(B) 0,25 P

(C) 1,25P

(D) 0,75P

(E) P

Considere que o novo quadrado possui lados iguais a x, onde o perímetro é P, ou 4x.

Como o quadrado foi criado duplicando a largura e reduzindo à metade o comprimento, podemos concluir que a largura anterior era x/2 e o comprimento era 2x.

Calculando o perímetro do retângulo:

x/2 + x/2 + 2x + 2x = 5x

 

Como 4x = P, temos que:

5x = 4x + x = P + P/4 = 5P/4 = 1,25P

 

Resposta: C

 

 

60. Em cada um dos quadrados menores que formam o quadrado da Figura a seguir será colocado um dos números 1, 2 ou 3, de modo que não haja números repetidos na mesma linha nem números repetidos na mesma coluna.

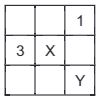
A soma dos números representados pelas letras X e Y da Figura vale

(A) 6

(B) 2

(C) 5

(D) 3

(E) 4

 

Resolução

Completando o quadrado, de modo que números iguais não apareçam na mesma linha ou coluna, temos:

2  3  1

3  1   2

1   2  3

 

Veja que x = 1 e y = 3.

x + y = 4

 

Resposta: E