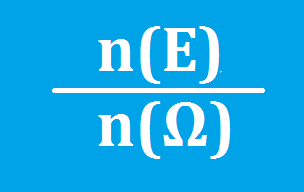Confira aqui um super resumo, bem objetivo, sobre o cálculo de probabilidade, onde apresentamos algumas definições, a razão da probabilidade e vários exemplos.
O conteúdo é muito cobrado em concursos públicos e a matéria possui um nível de dificuldade alto, principalmente porque utiliza os conceitos de análise combinatória.
Bom Estudo!
INTRODUÇÃO
Estudar a probabilidade é analisar as possibilidades de ocorrência de um determinado fato. Podemos analisar as chances de uma pessoa ganhar na Mega-Sena, de sofrer um acidente de avião, de ganhar dinheiro em uma mesa de cassino ou de acertar o resultado de uma partida de futebol.
É muito importante que se diga que a Teoria da Probabilidade não tem como objetivo acertar o resultado de determinado experimento, e sim de calcular as chances deste acontecer.
Para determinarmos essas possibilidades utilizamos a razão de probabilidade que veremos a seguir, após aprendermos alguns conceitos.
EXPERIMENTOS ALEATÓRIOS
Quando lançamos uma moeda, não há como prever o resultado, sabemos apenas que existem duas opções, cara ou coroa.
Da mesma forma, quando lançamos um dado, temos 6 possibilidades distintas.
Experimentos como esses recebem o nome de “experimentos aleatórios”, pois quando repetidos em condições idênticas, apresentam diferentes resultados que não podem ser previstos.
ESPAÇO AMOSTRAL
Dado um experimento aleatório, o conjunto de todos os resultados possíveis desse experimento é denominado espaço amostral e é representado pela letra grega Ω (ômega).
O número de elementos de um espaço amostral será representado por n(Ω).
Exemplo 1. Lançamento de uma moeda honesta.
Ω = {cara, coroa}
n(Ω) = 2
Exemplo 2. Lançamento de um dado honesto.
Ω = {1, 2, 3, 4, 5, 6}
n(Ω) = 6
EVENTO
Na probabilidade, chamamos de evento a todo subconjunto do espaço amostral. Utilizando os exemplos anteriores, podemos chamar de eventos a ocorrência de “coroa” ao lançarmos uma moeda e a ocorrência no lado “5”, no lançamento de um dado. Esses eventos podem ser representados da seguinte forma:
E = {coroa}
E = {5}
RAZÃO DE PROBABILIDADE
Chamamos de razão de probabilidade a fórmula utilizada para o cálculo das possibilidades de um evento ocorrer, quando levamos em conta o seu espaço amostral.
Como o próprio nome já diz, trata-se de uma fração, onde o numerador é igual ao número de elementos do evento, e o denominador é igual a quantidade de elementos do espaço amostral. Veja:
Onde:
E = evento
p(E) = probabilidade de um evento ocorrer
n(E) = número de casos favoráveis
Ω = espaço amostral
n(Ω) = número de elementos do espaço amostral (número de casos possíveis)
Exemplo 3. Calcular a probabilidade de sair os números 4 ou 5 no lançamento de um dado.
Temos:
n(E) = 2 (quantidade de casos favoráveis)
n(Ω) = 6 (quantidade de elementos do espaço amostral)
Exemplo 4. Calcular a probabilidade de, ao lançarmos uma moeda três vezes consecutivas, ocorrer cara apenas uma única vez.
Vejamos no diagrama de árvore todas as possibilidades:
Nele é possível ver que:
– a quantidade de casos favoráveis é 3: (cara, coroa, coroa); (coroa, cara, coroa); (coroa, coroa, cara).
– a quantidade de casos possíveis é 8.