Nesta página vamos abordar os tipos de funções (sobrejetora, injetora e bijetora). Sugerimos que o aluno já tenha um bom conhecimento acerca de conjuntos e da definição de função, principalmente os conceitos de domínio, imagem e contradomínio.
Bom estudo!
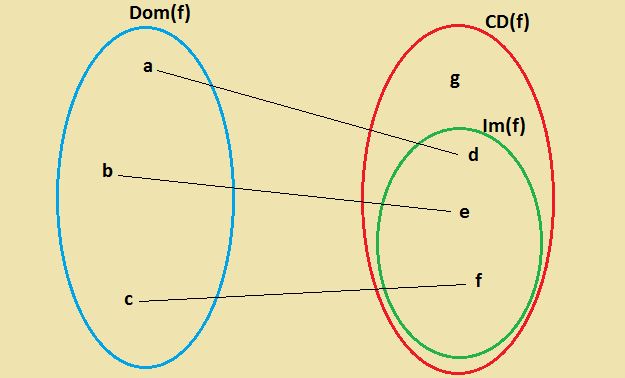
FUNÇÃO SOBREJETORA
Uma função f:A → B é dita sobrejetora quando, para todo y pertencente ao conjunto B, existe um x pertencente ao conjunto A que se relaciona com ele. Neste caso, temos que a imagem de f é igual ao conjunto B. Para facilitar, podemos dizer que a função sobrejetora é aquela em que ninguém “sobra” em B.
Exemplo de uma função sobrejetora:
Seja f a função de A = {1, 2, 3} em B = {2, 4, 6}, definida pela lei f(x) = 2x.
Observe que para cada um dos elementos de B, existe um elemento de A associado a ele.
Temos também que o contradomínio e a imagem são iguais:
Domínio: D(f) = {1, 2, 3}
Contradomínio: CD(f) = {2, 4, 6}
Imagem: Im(f) = {2, 4, 6}
Exemplo de função não sobrejetora:
Seja f a função de A = {1, 2, 3} em B = {2, 3, 6, 9}, definida pela lei f(x) = 3x.
Observe que existe um elemento “sobrando” em B, o elemento 2 não está associado a nenhum elemento do conjunto A.
Temos também que o contradomínio e a imagem são diferentes:
Domínio: D(f) = {1, 2, 3}
Contradomínio: CD(f) = {2, 4, 6, 9}
Imagem: Im(f) = {3, 6, 9}
FUNÇÃO INJETORA
Uma função f:A → B é dita injetora quando, para todo y pertencente ao conjunto B, existe no máximo um x pertencente ao conjunto A que se relaciona com ele.
Exemplo de função injetora:
Seja f a função de A = {3, 4, 5} em B = {13, 14, 15, 16}, definida pela lei f(x) = x + 10.
Observe que para cada um dos elementos de B, existe no máximo um elemento de A associado a ele.
Nesta função temos:
Domínio: D(f) = {3, 4, 5}
Contradomínio: CD(f) = {13, 14, 15, 16}
Imagem: Im(f) = {13, 14, 15}
Exemplo de função não injetora:
Seja f a função de A = {-2, 2, 3} em B = {4, 5, 9}, definida pela lei f(x) = x².
Observe que existe um elemento do conjunto B que está associado a dois elementos do conjunto A. Temos:
f(-2) = 4
f(2) = 4
Nesta função temos:
Domínio: D(f) = {-2, 2, 3}
Contradomínio: CD(f) = {4, 5, 9}
Imagem: Im(f) = {4, 9}
FUNÇÃO BIJETORA
Com certeza você já deve ter se perguntado se uma função pode ser sobrejetora e injetora ao mesmo tempo não é? A resposta é sim. E sempre que uma função for sobrejetora e injetora, temos um nome especial para ela, dizemos que é uma função bijetora. Simples assim.
Exemplo de função bijetora:
Seja f a função de A = {0, 1, 2} em B = {1, 3, 5}, definida pela lei f(x) = 2x + 1.
Observe que existe para cada elemento do conjunto B, existe um, e apenas um, elemento de A que está associado a ele.
Nesta função temos:
Domínio: D(f) = {0, 1, 2}
Contradomínio: CD(f) = {1, 3, 5}
Imagem: Im(f) = {1, 3, 5}
Gostou do nosso conteúdo sobre função sobrejetora, injetora e bijetora? Curta e compartilhe nas redes sociais.