Está estudando sobre as funções? Confira aqui nossa lista de exercícios resolvidos sobre os tipos de função (sobrejetora, injetora e bijetora).
Todos os exercícios foram retirados de concursos públicos realizados pelo país.
Bom estudo.
Questão 1 (Prefeitura Municipal de Canavieira – 2015). Sobre funções injetoras, sobrejetoras e bijetoras, julgue os itens abaixo em verdadeiro ou falso.
I. Toda função injetora é bijetora.
II. Quando elementos diferentes geram imagens diferentes,temos uma função sobrejetora.
III.Toda função bijetora admite inversa.
VI. Quando a imagem é igual ao contra domínio temos uma função sobrejetora.
a) V V V V
b) F F V V
c) V V F F
d) F F F F
Resolução
Vamos analisar caso a caso:
I – Falso
Uma função pode ser injetora, porém existir um elemento no contradomínio que não esteja associado a um elemento do domínio, fato este que tornaria a função não sobrejetora e consequentemente não bijetora.
II – Falso
O fato do elemento do domínio estar associado a um elemento igual ou diferente no contradomínio não é determinante na classificação das funções.
III – Verdadeiro
Uma função é bijetora se e somente se possui uma função inversa.
IV – Verdadeiro
Se o contradomínio e a imagem são iguais, então todo elemento do contradomínio está associado a pelo menos um elemento do domínio e essa função é sobrejetora.
Resposta: B
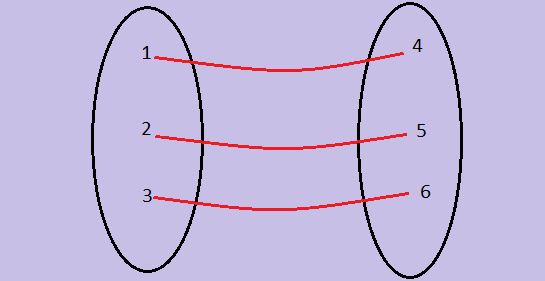
Questão 2 (Eletrobrás 2014). No figura a seguir está evidenciada, através de setas, uma relação entre os elementos do conjunto A e os elementos do conjunto B.
A respeito desta relação é correto afirmar que:
(A) não é uma função.
(B) é uma função que não é injetora nem sobrejetora.
(C) é uma função injetora, mas não sobrejetora.
(D) é uma função sobrejetora, mas não injetora.
(E) é uma função bijetora.
Resolução
Se o candidato se concentrar apenas no conjunto B, vai marcar de cara que é uma função bijetora pois cada elemento de B está associado a um, e apenas um, elemento de A.
A pegadinha está no elemento 5 do conjunto A, pois para ser uma função, cada elemento do conjunto A deve estar associado a um, e apenas um, elemento do conjunto B.
Resposta: A