Confira aqui vários exercícios resolvidos sobre comprimento de arco de circunferência, tópico básico da trigonometria.
O ideal é que o aluno já possua conhecimentos acerca de ângulos e transformação de graus em radianos.
Bom estudo a todos.
Exercício 1. Calcular o comprimento do arco cujo ângulo central é 0,3π e o raio da circunferência é igual a 6 cm.
C = α.r
C = 0,3π . 6
C = 0,3 . 3,14 . 6
C = 5,65 cm
Exercício 2. Calcular o comprimento do arco cujo ângulo central é π e o raio da circunferência é igual a 9 cm.
C = α.r
C = π . 9
C = 3,14 . 9
C = 28,26 cm
Exercício 3. Calcular o comprimento do arco representado na figura abaixo:
C = α.r
C = 0,4π . 1
C = 0,4 . 3,14
C = 1,256 cm
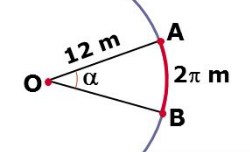
Exercício 4 (DEPEN 2013 – CESPE). Abaixo, a figura 1 apresenta o arco de circunferência AB correspondente ao ângulo central 2π/3 de uma circunferência de centro O e raio AO = 12 cm e a figura 2 apresenta alguns triângulos. A partir dessas informações e considerando que XY denote a distância entre os pontos X e Y, considere, ainda, as seguintes proposições:
U: o comprimento do arco AB é maior do que OA + OB
V: QR + RP + PS < QP + PS
Com base nas informações e nas figuras acima apresentadas e tomando 3,14 como valor aproximado de π, julgue a afirmação: “A proposição U ⇒ V é falsa”
Resolução:
Analisando a tabela verdade condicional, para que a proposição seja falsa, é necessário que U seja verdadeira e V seja falsa.
Analisando a proposição U:
Como a circunferência tem raio igual a 12cm:
OA + OB = 24cm.
Calculando o tamanho do arco AB:
C = (2π/3).r = (2.3,14/3).12 = 25,12cm
Logo, a proposição U é verdadeira.
Analisando a proposição V:
Utilizando as desigualdades triangulares temos que QP < QR + RP
Somando PS em ambos os lados:
QP + PS < QR + RP + PS
Daí, a proposição V é Falsa.
Como U é uma proposição verdadeira e V é uma proposição Falsa, podemos concluir que a proposição U ⇒ V é falsa.
Resposta: CERTO
Gostou dos nossos exercícios resolvidos sobre comprimento de arco?
Deixe o seu comentário.