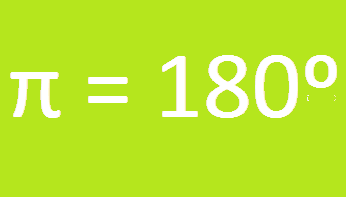Continuando o estudo da trigonometria, vamos falar um pouco sobre a circunferência trigonométrica, em especial a conversão de graus para radianos e vice versa.
É muito importante que o estudante já tenha conhecimentos sobre ângulos e regra de três.
Bom estudo.
O GRAU
A unidade de medida mais utilizada para medir ângulos ou arcos de circunferência é o grau, cujo símbolo utilizado é o “º”.
Por definição, uma circunferência possui 360º, o que nos leva a concluir que 1/360 dela corresponde a 1º, chamado de arco unitário.
Veja a figura:
O RADIANO
O radiano (escreve-se rad) é a razão entre o comprimento de um arco e o seu raio.
Sabendo que o comprimento de uma circunferência pode ser calculado pela fórmula C = 2.π.r, a medida de uma circunferência, em radianos é dada por:
Daí, podemos concluir que:
2π rad = 360º
π rad = 180º
π/2 rad = 90º
π/4 rad = 45º
…
Veja como fica a circunferência medida em radianos:
E agora vem a grande pergunta:
COMO CONVERTER GRAUS EM RADIANOS E VICE VERSA?
Simples. Basta compararmos as duas circunferências. Como são grandezas diretamente proporcionais, podemos sempre utilizar a regra de três simples, utilizando 180º = π. Veja os exemplos:
Exemplo 1: Converter 60º em radianos.
Vamos utilizar a regra de três, onde x será a medida de 60º em radianos:
180º ———– π rad
60º ———– x
Exemplo 2: Converter 300º em radianos.
Vamos utilizar a regra de três, onde x será a medida de 300º em radianos:
180º ———– π rad
300º ———– x
Exemplo 3: Converter 3π/4 rad em graus.
Utilizando a regra de três, onde x é a medida em graus:
180º ———– π rad
x ———– 3π/4
Gostou da nossa página sobre como transformar graus em radianos?
Deixe o seu comentário.