Confira aqui como é calculado o ângulo entre duas retas concorrentes no plano cartesiano.

Não deixe de ver também nossos conteúdos sobre os outros tópicos da geometria analítica.

Bom estudo!

 

 

Sejam r e s duas retas distintas e concorrentes, ambas oblíquas aos eixos coordenados e não perpendiculares entre si. Veremos abaixo como determinar o ângulo agudo entre as retas, simbolizado por θ.

 

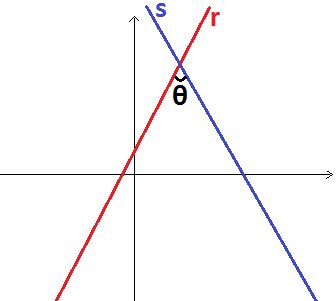
Considere que as equações reduzidas das retas r e s são:

r: y = m₁.x + n₁

s: y = m₂.x + n₂

 

Sendo m₁ e m₂ os coeficientes angulares das retas r e s, respectivamente, podemos calcular o ângulo θ através da fórmula abaixo:

 

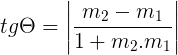
Pela fórmula é possível observar que:

• Se as retas forem paralelas, teremos m₂ – m₁ = 0, e θ = 0º.
• Se as retas forem perpendiculares, teremos m₂.m₁ = -1, fazendo com que o denominador seja igual a zero. Por isso a restrição quanto às retas serem perpendiculares.

 

 

Caso Especial

Quando estudamos a equação geral da reta vimos que uma reta pode ser vertical. Neste caso, quando uma das retas for vertical e a outra oblíqua, podemos calcular o ângulo θ formado entre elas através da seguinte fórmula:

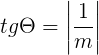
Neste caso, m é o coeficiente angular da reta que não é vertical.

 

 

Exemplo 1. Calcular o ângulo agudo formado pelas retas r: y = 3x + 1 e s: y = -2x – 1.

Sendo θ o ângulo agudo formado pelas retas r e s, e observando nas equações reduzidas que os coeficientes angulares  de r e s são, respectivamente, 3 e -2, temos:

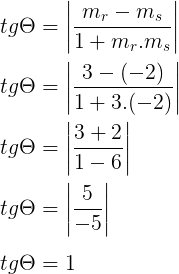
Como θ é um ângulo agudo e tgθ = 1, temos que θ = 45º.

 

 

Exemplo 2. Calcular o ângulo agudo formado pelas retas r: y = 2x e s: y = -x + 6.

Temos que os coeficientes das retas r e s são, respectivamente, 2 e -1.

Sendo θ o ângulo agudo entre r e s, temos:

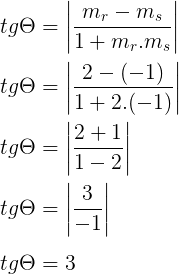
Portanto, θ = arctg3, onde 0º < θ < 90º.

 

 

Exemplo 3. Calcular o ângulo agudo formado pelas retas r: y = -x + 2 e s: x = 3.

Trata-se de um caso especial pois a reta s é vertical.

É possível observar também que o coeficiente angular da reta r é -1.

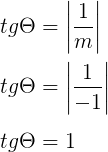
Daí, θ = 45º.

 

 

Gostou do nosso conteúdo sobre ângulos entre retas?

Deixe o seu comentário. Sua opinião é fundamental para o nosso site.