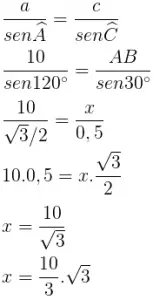Continuando a falar sobre a temida trigonometria, abordaremos a lei do seno, ferramenta utilizada no estudo de triângulos que não são retângulos.
Pede-se que o aluno já tenha algum conhecimento sobre as razões trigonométricas e geometria plana.
Bom estudo!
A lei dos senos relaciona lados e ângulos em um triângulo não retângulo, onde não é possível utilizar ferramentas mais conhecidas, como por exemplo, o teorema de Pitágoras.
Seja ABC um triângulo qualquer, cujos ângulos internos α, β, θ, e cujos lados medem a, b e c. Veja a figura:
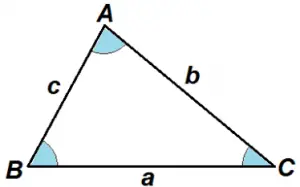
Pela lei do seno, valem as seguintes relações:
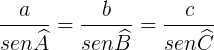
VAMOS PRATICAR?
Exemplo 1: Calcule a medida de AB no triângulo abaixo:
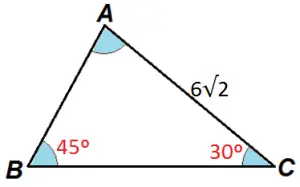
Considerando que temos um triângulo qualquer, vamos utilizar a lei dos senos:
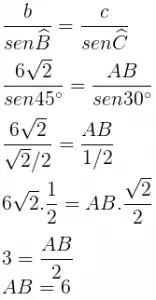
Exemplo 2: Sabendo que sen40º = 0,64 e sen60º = 0,87, calcule o valor de x no triângulo abaixo:
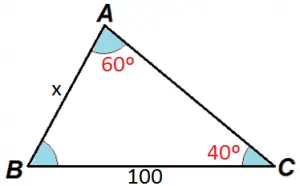
Tratando-se de um triângulo qualquer, vamos utilizar a lei dos senos:
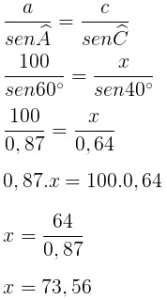
Exemplo 3: Descubra a medida de AB no triângulo abaixo:
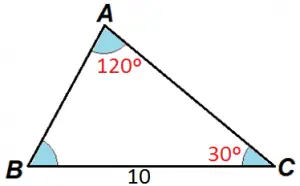
Utilizando a lei dos senos: