Procurando a prova resolvida do concurso para Analista Judiciário do TRT 9ª Região, aplicada em 2015 pela FCC?

Chegou ao site certo.

Aqui você encontra todas as questões de Matemática e Raciocínio Lógico-Matemático resolvidas e comentadas.

Bons estudos.

 

 

 

Questão 16. Um escritório comprou canetas, corretivos e arquivos pagando por cada unidade, respectivamente, R$ 1,00, R$ 3,00 e R$ 10,00.

Sabendo-se que o gasto total na compra foi de R$ 220,00 e que foram adquiridos ao menos uma unidade de cada produto, é necessariamente correto concluir que a compra incluiu, no

(A) máximo, 70 corretivos.

(B) máximo, 203 canetas.

(C) máximo, 21 arquivos.

(D) mínimo, 2 corretivos.

(E) mínimo, 2 canetas.

 

Resolução:

Vamos resolver a questão por eliminação:

 

(A) máximo, 70 corretivos.

Resposta errada.

Se o escritório comprar 70 corretivos, como o custo unitário é de 3,00, já haveria um gasto de 210 reais somente com corretivos.

Como foram adquiridos ao menos uma unidade de cada produto, temos que o valor irá passar de 220 reais.

 

(B) máximo, 203 canetas.

Resposta errada.

O escritório poderia comprar, por exemplo, 207 canetas, 1 corretivo e 1 arquivo, que daria 220 reais.

 

(C) máximo, 21 arquivos.

Resposta correta.

O escritório poderia comprar 21 arquivos (210 reais) e utilizar os 10 reais restantes para comprar canetas e corretivos, como bem entender.

Repare que caso compre 22 arquivos, o valor total já seria de 220 reais.

 

(D) mínimo, 2 corretivos.

Resposta errada.

O escritório poderia comprar 1 corretivo, 7 canetas e 21 arquivos, que daria 220 reais.

 

(E) mínimo, 2 canetas.

Resposta errada.

O escritório poderia comprar 1 caneta, 3 corretivos e 21 arquivos, que daria 220 reais.

 

 

 

Questão 17. Um juiz tem que analisar x processos nos próximos y dias de trabalho. Se ele decidir analisar, a partir do primeiro dia, 4 processos por dia de trabalho, no último dos y dias ele só terá que analisar 3 processos. Por outro lado, se ele decidir analisar, a partir do primeiro dia, 3 processos por dia de trabalho, no último dos y dias ele terá que analisar 24 processos. Nas condições descritas, x + y é igual a

(A) 109.

(B) 101.

(C) 83.

(D) 99.

(E) 93.

 

Resolução:

Vamos analisar as duas opções que o juiz tem:

 

Primeira:

“ 4 processos por dia de trabalho, no último dos y dias ele só terá que analisar 3 processos”

Veja que se ele analisar 4 por dia, no último dia irá faltar um processo.

Podemos montar a seguinte equação:

x = 4y – 1

 

Segunda:

“ 3 processos por dia de trabalho, no último dos y dias ele terá que analisar 24 processos”

Veja que se ele analisar 3 por dia, no último dia irá sobrar 21 processos, por isso ficam 24 para o último dia.

Podemos montar a seguinte equação:

x = 3y + 21

 

Subtraindo a segunda da primeira equação:

x – x = 4y – 1 – 3y – 21

0 = y – 22

y = 22

 

Utilizando a primeira equação para achar o valor de x:

x = 4y – 1

x = 4.22 – 1

x = 88 – 1

x = 87

 

Resposta:

x + y = 87 + 22 = 109

 

 

 

Questão 18. Renato quer comprar dois livros em uma livraria, porém, seu dinheiro é suficiente apenas para levar o mais caro, com sobra de R$ 22,00, ou o mais barato, com sobra de R$ 38,00. Como incentivo à leitura, o dono da livraria deu um desconto de R$ 10,00 na compra total dos dois livros e Renato conseguiu levá-los sem que sobrasse ou faltasse dinheiro. Nas condições descritas, o desconto percentual sobre o valor correto da compra que o dono da livraria deu para Renato foi de

(A) 8,5%.

(B) 10%.

(C) 12,5%.

(D) 8%.

(E) 9,5%.

 

Resolução:

 

Sejam:

x o valor do mais caro

y o valor do mais barato

z a quantia que Renato tinha

 

Da informação:

“ seu dinheiro é suficiente apenas para levar o mais caro, com sobra de R$ 22,00”

Podemos montar a seguinte equação:

z = x + 22

 

Da informação:

“o mais barato, com sobra de R$ 38,00”

Podemos montar a seguinte equação:

z = y + 38

 

Da informação:

“ desconto de R$ 10,00 na compra total dos dois livros e Renato conseguiu levá-los sem que sobrasse ou faltasse dinheiro”

Podemos montar a seguinte equação:

z + 10 = x + y

 

Temos três equações.

 

Subtraindo a terceira da primeira equação:

z – z – 10 = x + 22 – x – y

– 10 = 22 – y

y = 22 + 10

y = 32

 

Subtraindo a terceira da segunda equação:

z – z – 10 = y + 38 – x – y

– 10 = 38 – x

x = 38 + 10

x = 48

 

Achamos o valor correto dos livros.

O mais caro custa 48 reais e o mais barato 32 reais.

Total de 80 reais.

 

Sabendo-se o desconto foi de 10 reais, vamos calcular o desconto percentual:

 

10/80 = 1/8 = 0,125 = 12,5%

 

 

 

Questão 19. Carolina, Cecília, João, Sérgio e Sílvia formaram um grupo musical. Durante cada apresentação do grupo, um deles canta e os outros quatro tocam um instrumento diferente cada um (bateria, guitarra, teclado e saxofone), de acordo com as seguintes condições:

− Carolina só pode tocar bateria ou guitarra;

− Cecília só pode cantar ou tocar saxofone;

− João só pode tocar teclado ou saxofone;

− Sérgio só pode cantar, ou tocar bateria, ou tocar teclado;

− Sílvia só pode cantar ou tocar guitarra.

Se Sílvia foi escolhida para cantar em uma apresentação então, necessariamente, nessa apresentação

(A) Carolina tocará bateria.

(B) Sérgio tocará bateria.

(C) João tocará saxofone.

(D) Sérgio tocará teclado.

(E) Cecília tocará guitarra.

 

Resolução:

 

Se Sílvia foi escolhida para cantar, e como “ Cecília só pode cantar ou tocar saxofone”, então Cecília irá tocar saxofone.

 

Se Cecília irá tocar saxofone, e como “ João só pode tocar teclado ou saxofone”, então João irá tocar teclado.

 

Se João irá tocar teclado, e como “Sérgio só pode cantar, ou tocar bateria, ou tocar teclado”, então Sérgio irá tocar bateria (já sabemos que Sílvia irá cantar).

 

 

 

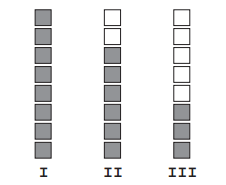
Questão 20. A figura indica o marcador de combustível de um carro em três instantes diferentes (I, II, III). No instante I o motorista havia acabado de completar o tanque de combustível do carro, que tem capacidade de 60 litros. O instante II representa quando o carro completou x quilômetros percorridos depois do abastecimento no instante I. O instante III representa quando o carro completou y quilômetros depois do abastecimento no instante I.

 

 

 

 

 

 

Considerando que o consumo médio de combustível desse carro de I até II foi de 12 quilômetros por litro, e de I até III foi de 10 quilômetros por litro, então, a distância percorrida pelo carro de II até III, em quilômetros, foi igual a

(A) 170.

(B) 215.

(C) 205.

(D) 195.

(E) 185.

 

Resolução:

Na figura percebemos que o marcador de combustível foi dividido em 8 partes.

Como a capacidade é de 60 litros, cada parte representa 7,5 litros.

 

Do trecho I ao II, o carro consumiu 2/8 do tanque, ou seja, 15 litros.

Como o consumo foi de 1 litro a cada 12 km, então o carro percorreu:

15 x 12 = 180km

 

Do trecho I para o III, o carro consumiu 5/8 do tanque, ou seja, 37,5 litros.

Como o consumo foi de 1 litro a cada 10 km, então o carro percorreu:

10 x 37,5 = 375km

 

Logo, a distância percorrida de II até III será:

375 – 180 = 195km

 

 

 

Comentários sobre a prova:

Esperamos ter ajudado com mais uma prova do TRT 9ª Região resolvida. Desta vez a Fundação Carlos Chagas não cobrou teorias e fórmulas matemáticas. Foi possível resolver todas as questões através de deduções e lógica. A dica para as próximas provas da FCC é focar nas questões de raciocínio lógico.

Não se esqueça de deixar seu comentário sobre a prova e sobre a resolução das questões.

Boa sorte.