Estudando matemática para o concurso da SAP SP? Confira aqui a prova resolvida do concurso realizado em 2013 pela VUNESP para o cargo de Agente de Segurança Penitenciária.

Veja também em nosso menu outras provas resolvidas de concursos para o Estado de SP e da banca Vunesp.

Bom estudo!

 

 

26. Uma pessoa comprou um produto exposto na vitrine por um valor promocional de 20% de desconto sobre o preço P do produto. Como ela pagou em dinheiro, teve mais 10% de desconto sobre o valor promocional. Então, essa pessoa pagou, sobre o preço P do produto, um valor igual a

(A) 0,28P.

(B) 0,03P.

(C) 0,7P.

(D) 0,3P.

(E) 0,72P

 

Seja P o valor do produto.

Como estava na promoção com 20%, o preço passou a ser de 0,8.P (80% do valor).

Ao pagar em dinheiro, o comprador ganhou mais 10% e o preço passou a ser 0,8P.0,9(90% do valor):

0,8P.0,9 = 0,72.P

 

 

27. Uma pizzaria funciona todos os dias da semana e sempre tem promoções para seus clientes. A cada 4 dias, o cliente tem desconto na compra da pizza de calabresa; a cada 3 dias, na compra de duas pizzas, ganha uma mini pizza doce, e uma vez por semana tem a promoção de refrigerantes. Se hoje estão as três promoções vigentes, esse ocorrido voltará a acontecer daqui a quantas semanas?

(A) 40.

(B) 12.

(C) 84.

(D) 22.

(E) 7.

 

Veja que os descontos acontecem a cada, 4, 3 e 7 dias.

Hoje é o dia da coincidência. Queremos saber quando acontecerá novamente.

Na verdade estamos querendo saber qual o menor múltiplo comum de 4, 3 e 7, ou seja, o mmc e 4, 3 e 7, que é 84.

Para descobrirmos a semana, obviamente basta dividir por 7:

84/7 = 12

 

 

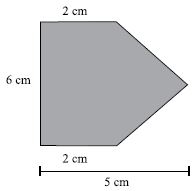
28. Ricardo esteve em um lançamento imobiliário onde a maquete, referente aos terrenos, obedecia a uma escala de 1:500. Ricardo se interessou por um terreno de esquina, conforme mostra a figura da maquete.

A área, em metros quadrados, desse terreno é de

(A) 300.

(B) 755.

(C) 120.

(D) 525.

(E) 600.

 

Primeiramente, vamos utilizar a escala 1:500 para sabermos as dimensões reais do terreno:

2cm equivale a 2.500 = 1000cm = 10m

6cm equivale a 6.500 = 3000cm = 30m

5cm equivale a 5.500 = 2500cm = 25m

 

Sabendo disto, para calcularmos a área é muito simples, basta dividirmos a figura em duas, um retângulo e um triângulo:

O retângulo terá base 30m (6cm) e altura 10m (2cm):

Área = 30×10 = 300m²

O triângulo terá base 30m (6cm) e altura 15m (3cm):

Área  = 30×15/2 = 225m²

 

Área total = 300 + 225 = 525m²

 

 

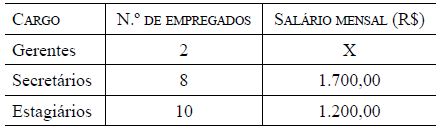
29. Em uma seção de uma empresa com 20 funcionários, a distribuição dos salários mensais, segundo os cargos que ocupam, é a seguinte:

Sabendo-se que o salário médio desses funcionários é de R$ 1.490,00, pode-se concluir que o salário de cada um dos dois gerentes é de

(A) R$ 2.900,00.

(B) R$ 4.200,00.

(C) R$ 2.100,00.

(D) R$ 1.900,00.

(E) R$ 3.400,00.

 

Vamos calcular a média ponderada:

(2x + 8.1700 + 10.1200)/20 = 1490

2x + 13600 + 12000 = 1490.20

2x + 25600 = 29800

2x = 29800 – 25600

2x = 4200

x = 4200/2

x = 2100

 

 

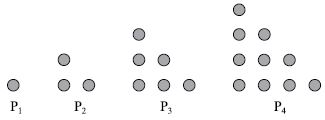
30. Observe a sequência de figuras com bolinhas.

Mantendo-se essa lei de formação, o número de bolinhas na 13.a posição (P13) será de

(A) 91.

(B) 74.

(C) 63.

(D) 58.

(E) 89.

 

Repare que:

P1 = 1

P2 = 1 + 2

P3 = 1 + 2 + 3

…

P13 = 1 + 2 + 3 + … + 12 + 13

Basta somarmos os termos dessa PA, onde a1 = 1, a13 = 13 e n = 13

Pela fórmula da soma de uma PA:

S = (a1 + an).n/2

S = (1 + 13). 13/2

S = 14.13/2

S = 91

 

 

31. Em uma papelaria há duas máquinas de xerox. Uma é mais nova e mais rápida do que a outra. A produção da máquina antiga é igual a 1/3 da produção da máquina mais nova. Em uma semana, as duas máquinas produziram juntas 3 924 folhas xerocadas. Dessa quantidade, o número de folhas que a máquina mais rápida xerocou é

(A) 1 762.

(B) 2 943.

(C) 1 397.

(D) 2 125.

(E) 981.

 

As duas juntas produziram 3924 folhas.

Como uma é 1/3 mais rápida que a outra, a cada 4 folhas, 1 foi feita pela lenta e 3 foram feitas pela rápida.

Vamos calcular quantas a rápida fez:

3924.3/4 = 2943

 

 

32. Para resgatar, no mínimo, o triplo de um capital aplicado a juro simples, à taxa de 5% a.m., o tempo, em meses, que uma pessoa tem de esperar é

(A) 30.

(B) 50.

(C) 10.

(D) 20.

(E) 40.

 

Fórmula de juros simples:

M = C.(1 + in), onde:

M = montante

C = Capital inicial

i = taxa

n = quantidade de períodos

 

Como queremos que o capital inicial passe de C a 3C, temos:

3C = C(1 + 0,05n)

3 = 1 + 0,05n

3 – 1 = 0,05n

0,05n = 2

n = 2/0,05

n = 40

 

 

33. Uma competição de corrida de rua teve início às 8h 04min. O primeiro atleta cruzou a linha de chegada às 12h 02min 05s. Ele perdeu 35s para ajustar seu tênis durante o percurso. Se esse atleta não tivesse tido problema com o tênis, perdendo assim alguns segundos, ele teria cruzado a linha de chegada com o tempo de

(A) 3h 58min 05s.

(B) 3h 57min 30s.

(C) 3h 58min 30s.

(D) 3h 58min 35s.

(E) 3h 57min 50s.

 

Início: 8h 04min

Chegada: 12h 02min 05s

Diferença: 3h 58min 05s

Que descontando os 35s do tênis:

3h 57min 30s

 

 

34. Em uma academia foi realizada uma enquete em que as pessoas tinham que indicar um setor onde eles mais frequentavam, dentre os três indicados no questionário: musculação, condicionamento físico ou natação. Cada uma dessas pessoas também precisou optar por apenas um tipo de alimentação, a qual acreditava ser mais importante após os treinos, dentre as duas oferecidas: carboidratos ou fibras. Os resultados das escolhas estão na tabela a seguir:

Nas condições apresentadas na tabela, pode-se afirmar que

(A) 50% do total de pessoas optaram por Fibras e Natação.

(B) 12% dos que escolheram Fibras optaram por Musculação.

(C) 40% dos que escolheram Carboidratos optaram por Condicionamento Físico.

(D) 30% dos que escolheram Carboidratos optaram por Musculação.

(E) 20% do total de pessoas optaram por Fibras e Condicionamento Físico.

 

Repare que 70 pessoas escolheram carboidratos, e dessas, 28 escolheram condicionamento físico.

28/70 = 0,4 = 40%

Resposta: C

 

 

35. O dono de uma fábrica irá instalar cerca elétrica no estacionamento que tem forma retangular de dimensões 100 m por 140 m. Também, por motivo de segurança, pretende, a cada 40 metros, instalar uma câmera. Sendo assim, ele utilizará de cerca elétrica, em metros, e de câmeras, respectivamente,

(A) 480 e 12.

(B) 380 e 25.

(C) 420 e 53.

(D) 395 e 30.

(E) 240 e 40.

 

Calculando o perímetro do retângulo:

100 + 100 + 140 + 140 = 480m

Calculando quantas câmeras serão utilizadas em 480m, sabendo que tem uma a cada 40m:

480/40 = 12

 

 

36. Uma piscina tem a forma de um bloco retangular de base quadrada. Sua altura mede 2,8 m e o lado da base quadrada mede 11 m. A piscina deve conter, no máximo, 3/4 de água para que as pessoas possam entrar e essa não transbordar. Assim sendo, a quantidade máxima de litros de água que essa piscina pode conter é

(A) 338,8.

(B) 220,5.

(C) 400,5.

(D) 308,0.

(E) 254,1.

 

Calculando o volume da piscina:

11 x 11 x 2,8 = 338,8m³

 

338,8.3/4 = 254,1m³

Obs: No gabarito consta letra E, mas claramente confundiram, pois 1m³ equivale a 1000 litros.

 

 

37. Uma loja tinha 150 televisões de um modelo que estava para sair de linha. Dessas, foram vendidas 3/5 e para acabar com essa mercadoria foi feita uma promoção de 10% de desconto do valor inicial para as televisões restantes. Foram vendidas todas as televisões e o valor total arrecadado foi de R$ 172.800,00. O preço de cada televisão com o desconto era de

(A) R$ 1.205,00.

(B) R$ 1.080,00.

(C) R$ 1.250,00.

(D) R$ 1.190,00.

(E) R$ 1.100,00.

 

Das 150 tvs, 3/5 foram vendidas sem desconto:

150.3/5 = 90

Nota-se que restaram 60, que foram vendidas com 10% de desconto.

Sendo x o preço inicial e cada tv, temos:

90x + 60.x.0,9 = 172800 (utilizamos o 0,9 para representar o desconto de 10%)

90x + 54x = 172800

144x = 172800

x = 172800/144

x = 1200 (esse é o preço inicial de cada tv)

 

Calculando o preço com o desconto:

1200.0,9 = 1080

 

 

38. Roberto irá cercar uma parte de seu terreno para fazer um canil. Como ele tem um alambrado de 10 metros, decidiu aproveitar o canto murado de seu terreno (em ângulo reto) e fechar essa área triangular esticando todo o alambrado, sem sobra. Se ele utilizou 6 metros de um muro, do outro muro ele irá utilizar, em metros,

(A) 7.

(B) 5.

(C) 8.

(D) 6.

(E) 9.

 

A questão fala em cercar um canto murado, utilizando 10m de tela. Veja na figura que temos claramente um triângulo retângulo. Basta utilizarmos o teorema de pitágoras, onde 10 é a hipotenusa, um cateto é 6 e o outro vamos chamar de x:

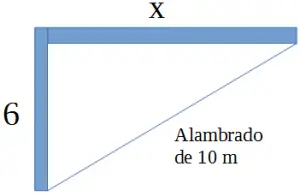
10² = 6² + x²

100 = 36 + x²

x² = 100 – 36

x² = 64

x = 8

 

 

39. Um arquiteto, em um de seus projetos, fez algumas medições e dentre elas mediu dois ângulos complementares. Um desses ângulos mediu 65º e o outro,

(A) 115º.

(B) 90º.

(C) 180º.

(D) 25º.

(E) 60º.

 

Lembrando que dois ângulos são complementares quando a soma é igual a 90º.

Chamando esse ângulo de x:

x + 65 = 90

x = 90 – 65

x = 25º

 

 

40. Uma máquina demora 1 hora para fabricar 4 500 peças. Essa mesma máquina, mantendo o mesmo funcionamento, para fabricar 3 375 dessas mesmas peças, irá levar

(A) 55 min.

(B) 15 min.

(C) 35 min.

(D) 1h 15min.

(E) 45 min.

 

Temos:

3375/4500 = 0,75 = 3/4 = 45min