Estudando matemática para concursos? Confira aqui a prova resolvida do concurso para a Polícia Militar do Estado de São Paulo (PM SP) realizado em 2014 pela Vunesp.

Veja em nosso menu outras provas resolvidas de concursos de carreiras policiais e da banca Vunesp.

Bom estudo!

21. Em um lote de xícaras de porcelana, a razão entre o número de xícaras com defeitos e o número de xícaras perfeitas, nesta ordem, é 2/3. Se o número total de xícaras do lote é 320, então, a diferença entre o número de xícaras perfeitas e o número de xícaras com defeitos, nesta ordem, é:

(A) 56.

(B) 78.

(C) 93.

(D) 85.

(E) 64.

Resolução

Vamos denominar:

x = número de xícaras com defeitos

y = número de xícaras perfeitas

Sabendo disto, temos as seguintes equações:

x/y = 2/3, ou seja, x = 2y/3

x + y = 320

Temos um sistema de equações de primeiro grau. Substituindo a primeira na segunda equação:

2y/3 + y = 320 (multiplicando ambos os lados por 3)

2y + 3y = 320.3

5y = 960

y = 960/5 = 192

Calculando x:

x = 2y/3 = 2.192/3 = 128

Logo,

y – x = 192 – 128 = 64

Resposta: E

22. Para irrigar uma horta, foram gastos 2/5 da água de um reservatório que estava totalmente cheio, e 1/3 da água restante foi utilizada para uso doméstico, restando, ainda, 50 litros de água dentro do reservatório. A capacidade total do reservatório, em litros, é:

(A) 155.

(B) 125.

(C) 100.

(D) 115.

(E) 140.

Resolução

Seja x a quantidade total do reservatório.

Após irrigar a horta com 2/5 de x restaram 3/5 de x, ou seja, 3x/5.

Após utilizar 1/3 do restante, restaram 2/3, ou seja, 2/3 de 3x/5, que equivale a 50 litros. Então:

2/3 de 3x/5 = 50

(2/3).(3x/5) = 50

2x/5 = 50

x = 50.5/2 = 250/2 = 125

Resposta: B

23. No estoque de uma papelaria, há uma caixa com várias borrachas iguais e, para facilitar as vendas, o dono dessa papelaria decidiu fazer pacotinhos, todos com a mesma quantidade de borrachas. Ao fazer isso, notou que era possível colocar 3 ou 4 ou 5 borrachas em cada pacotinho e, assim, não sobraria borracha alguma na caixa. O menor número de borrachas que essa caixa poderia conter era:

(A) 80.

(B) 65.

(C) 60.

(D) 70.

(E) 75.

Resolução

A questão fala de uma caixa com várias borrachas, onde o vendedor consegue dividir em caixas com 3, 4 ou 5 borrachas.

Estamos tratando de mmc (mínimo múltiplo comum), ou seja, a quantidade de borrachas pode ser dividida por 3, 4 ou 5 e tem que ser a menor possível.

Como não existem fatores primos em comum, o mmc(3, 4, 5) = 3.4.5 = 60

Resposta: C

24. Uma empresa, que está selecionando candidatos para preencher algumas vagas disponíveis, recebeu 320 currículos de candidatos interessados e selecionou 25% deles para uma entrevista. Sabendo que 10% dos candidatos selecionados para a entrevista faltaram, e que 25% dos que compareceram foram contratados, então, em relação ao número total de candidatos interessados e que enviaram o currículo, o número dos candidatos contratados representa, aproximadamente,

(A) 5,6%.

(B) 7,2%.

(C) 6,3%.

(D) 5,9%.

(E) 6,8%.

Resolução

Basta efetuarmos a multiplicação:

25% (selecionados). 90% (presentes) . 25% (contratados)

0,25 . 0,90 . 0,25 = 0,05625 = 5,625%

Resposta: A

25. Com um pote de sal um restaurante prepara vários pratos de sopa, cada um deles contendo 3 g de sal. Sabendo que o sal desse pote é utilizado somente no preparo da sopa, então, se em cada prato de sopa forem colocados apenas 2 g de sal, então, com a mesma quantidade de sal do pote será possível preparar 100 pratos de sopa a mais. A quantidade total de pratos que poderão ser preparados com apenas 2 g de sal em cada um é:

(A) 150.

(B) 200.

(C) 300.

(D) 350.

(E) 250.

Resolução

Vamos utilizar regra de três:

Gramas ————— Qtde pratos

3 ———————– x

2 ———————– x + 100

Repare que quanto mais gramas, menos pratos. São então grandezas inversamente proporcionais.

3x = 2(x + 100)

3x = 2x + 2.100

3x – 2x = 200

x = 200

Como a quantidade de pratos que podem ser feitos com 2g de sal é x + 100, a resposta só pode ser 200 + 100 = 300

Resposta: C

26. Três amigos, André, Bruno e Carlos foram a um rodízio de pizzas. Considerando-se o número total de pedaços de pizza consumidos pelos três amigos, juntos, na média, cada um comeu 7 pedaços. Sabendo-se que André e Bruno comeram o mesmo número de pedaços e que Carlos comeu 5 pedaços, o número de pedaços de pizza que André comeu foi:

(A) 6.

(B) 7.

(C) 10.

(D) 8.

(E) 9.

Resolução

Seja x a quantidade de pizzas que André e Bruno comeram (cada um).

Como Carlos comeu 5 pedaços e a média foi de 7 pedaços:

(André + Bruno + Carlos)/3 = 7

(x + x + 5)/3 = 7

2x + 5 = 3.7

2x = 21 – 5

2x = 16

x = 16/2 = 8

Resposta: D

27. Com determinada quantidade de dinheiro é possível comprar 5 revistas em quadrinhos, todas de mesmo valor e, ainda, sobram R$ 2,50. Porém, se com a mesma quantia de dinheiro forem compradas 7 revistinhas de palavras cruzadas, cada uma delas de mesmo valor, sobrarão R$ 0,50. Sabendo que uma revistinha de palavra cruzada custa R$ 1,00 a menos que uma revistinha em quadrinhos, então, o preço de uma revistinha de palavras cruzadas é:

(A) R$ 3,50.

(B) R$ 4,90.

(C) R$ 4,60.

(D) R$ 3,80.

(E) R$ 4,20.

Resolução

Seja x o valor de cada revista em quadrinhos e y o valor de cada palavra cruzada.

Pela afirmação: “é possível comprar 5 revistas em quadrinhos, todas de mesmo valor e, ainda, sobram R$ 2,50. Porém, se com a mesma quantia de dinheiro forem compradas 7 revistinhas de palavras cruzadas, cada uma delas de mesmo valor, sobrarão R$ 0,50.”, temos:

5x + 2,50 = 7y + 0,50

Pela afirmação: “uma revistinha de palavra cruzada custa R$ 1,00 a menos que uma revistinha em quadrinhos”, temos

y = x – 1,00

Note que temos duas equações com duas variáveis, ou seja, um sistema de primeiro grau. Substituindo a segunda na primeira equação:

5x + 2,50 = 7(x – 1,00) + 0,50

5x + 2,5 = 7x – 7 + 0,5

7x – 6,5 = 5x + 2,5

7x – 5x = 2,5 + 6,5

2x = 9

x = 9/2 = 4,50

Calculando y:

y = x – 1,00 = 4,50 – 1,00 = 3,50

Resposta: A

28. Uma pessoa foi a uma livraria e escolheu três livros: um romance, um de aventuras e um de ficção, porém, por motivos financeiros, decidiu que levaria apenas dois deles. Se comprar o romance e o livro de aventura, pagará R$ 53,00; se comprar o romance e o livro de ficção, pagará R$ 58,00 e, se comprar o livro de ficção e o livro de aventura, pagará R$ 55,00. O valor dos três livros juntos é:

(A) R$ 83,00.

(B) R$ 80,00.

(C) R$ 72,00.

(D) R$ 75,00.

(E) R$ 70,00.

Resolução

Seja R o valor do livro de romance, A o valor do de aventura e F o valor do de ficção.

Da afirmação: “Se comprar o romance e o livro de aventura, pagará R$ 53,00;”, temos:

R + A = 53

Da afirmação: “se comprar o romance e o livro de ficção, pagará R$ 58,00”, temos:

R + F = 58

Da afirmação: “se comprar o livro de ficção e o livro de aventura, pagará R$ 55,00”, temos:

F + A = 55

Vamos somar as três equações:

R + A + R + F + F + A = 53 + 58 + 55

2R + 2A + 2F =  166

2(R + A + F) = 166

R + A + F = 166/2

R + A + F = 83

Resposta: A

29. Um eletricista dispõe de 5,8 m de fio de cobre e, para realizar certo serviço, cortou 12 pedaços de 30 cm cada um. O restante do fio foi cortado em pedaços de 27,5 cm cada um, não restando pedaço algum de fio. O número de pedaços com 27,5 cm é:

(A) 6.

(B) 7.

(C) 9.

(D) 10.

(E) 8.

Resolução

Vamos calcular o tamanho dos 12 pedaços de 30 cm:

12 x 30 = 360 cm

Se ele tinha 580 cm (5,8 m), então sobraram 220 cm. Assim:

220 / 27,5 = 8

Resposta: E

30. Um escritório de advocacia precisa imprimir duas cópias de um mesmo documento, e a impressora disponível para realizar o serviço leva 12 segundos para imprimir cada uma das 50 páginas desse documento. Após imprimir a primeira cópia, com 50 páginas, foram feitos alguns ajustes e reparos nessa impressora, que passou a imprimir cada página desse documento em 9 segundos, o que fez com que o tempo gasto para imprimir as 50 páginas da segunda cópia desse documento fosse reduzido em

(A) 2 minutos e 50 segundos.

(B) 2 minutos e 30 segundos.

(C) 3 minutos e 30 segundos.

(D) 2 minutos e 05 segundos.

(E) 3 minutos e 50 segundos.

Resolução

Vamos calcular em quanto tempo a impressora imprimiu o primeiro documento:

(50 páginas) x (12 segundos) = 600 segundos = 10 minutos

Agora basta notar que na segunda cópia, a impressora passou a imprimir uma folha em 9 segundos e não mais em 12.

A velocidade aumentou em 3/12 = 0,25 = 25%

Então, o tempo de impressão da segunda cópia reduziu em 25%:

25% de 10 minutos = 10.25/100 = 2,5 minutos = 2 minutos e 30 segundos

Resposta: B

31. Uma sala retangular, com 8 m de comprimento por 5 m de largura, será dividida em duas salas menores: A e B, também retangulares, conforme mostra a figura.

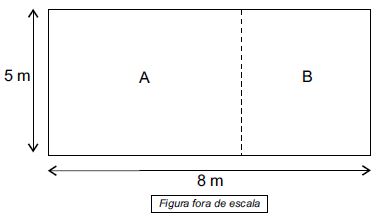
Sabendo que a área da sala A corresponde a 60% da área da sala original (antes da divisão) e, desprezando-se a espessura da parede que irá dividir as salas, pode-se concluir que o perímetro, em metros, da sala B será:

(A) 15,3.

(B) 16,2.

(C) 16,4.

(D) 15,8.

(E) 14,9.

Resolução

Se a sala A corresponde a 60%, então a sala B corresponde a 40%.

Veja que as larguras são iguais. A diferença está no comprimento, ou seja, o comprimento de B deve ser 40% de 8 m:

40% de 8 = 8.40/100 = 3,2 m

Calculando o perímetro:

5 + 5 + 3,2 + 3,2 = 16,4

Resposta: C

32. Uma pesquisa feita com 300 consumidores registrou a preferência de cada um deles sobre três marcas diferentes de sabonetes, conforme mostra a tabela.

Sabonete (marca) ——– Número de consumidores
marca A ———————– 90
marca B ———————– 75
marca C ———————- 120
Outras (O) ——————— 15

Considerando-se o número total de consumidores apresentados na tabela, o gráfico que representa essas informações, em porcentagem, é:

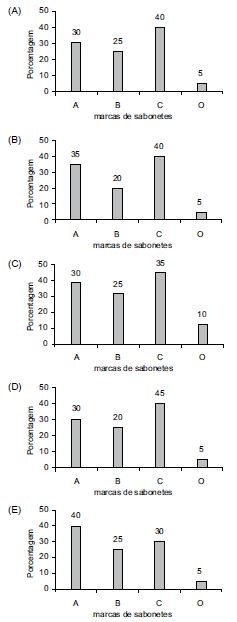
Resolução

Vamos calcular as porcentagens:

Marca A: 90/300 = 30%

Marca B: 75/300 = 25%

Marca C: 120/300 = 40%

Outras: 15/300 = 5%

Resposta: A

33. A grade lateral de um clube é formada por 85 barras de ferro que foram pintadas nas cores verde (V) e amarelo (A), obedecendo à ordem mostrada na figura.

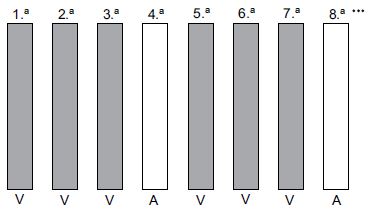
Sabendo que as cores se repetiram sempre nessa mesma sequência, o número de barras pintadas na cor verde foi:

(A) 64.

(B) 70.

(C) 68.

(D) 72.

(E) 74.

Resolução

São 85 barras e sempre aparecem 3 verdes em cada 4 barras, na ordem VVVA.

Primeiramente vamos observar que 84 é um múltiplo de 4, logo, 3 em cada 4 barras dessas 84 são verdes. Temos:

84.3/4 = 63

Basta somar mais uma barra, a de número 85.

Temos então 63 + 1 = 64 barras verdes.

Resposta: A

34. Um recipiente, na forma de um prisma reto de base quadrada, com 8 cm de lado, estava totalmente cheio de água. Desse recipiente foram retirados 160 mL, conforme mostra a figura.

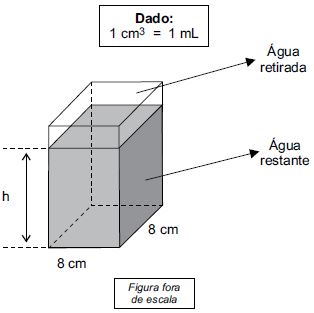
Sabendo que a capacidade máxima desse recipiente é 960 mL, então, após a retirada dos 160 mL, a altura h da água restante dentro dele, em cm, será de

(A) 12,0.

(B) 11,5.

(C) 11,0.

(D) 13,0.

(E) 12,5

Resolução

Foi dado que 1 cm³ equivale a 1 ml e que a capacidade máxima do recipiente é de 960 ml, ou seja, 960 cm³.

Para calcularmos o volume de um prisma, devemos multiplicar base x lado x altura. Repare que já sabemos o volume, vamos utilizar a fórmula para acharmos a altura:

base x lado x altura = 960

8 x 8 x altura = 960

64 x altura = 960

altura = 960 / 64

altura = 15 cm

No sólido geométrico em questão, o volume é proporcional a altura. Vamos calcular em porcentagem quanto o volume foi reduzido:

800/960 = 5/6 (o novo volume é 5/6 do volume total)

A altura também deve estar nessa proporção:

15 . 5/6 = 12,5 cm

Resposta: E

35. Duas estacas de madeira, perpendiculares ao solo e de alturas diferentes, estão distantes uma da outra, 1,5 m. Será colocada entre elas uma outra estaca de 1,7 m de comprimento, que ficará apoiada nos pontos A e B, conforme mostra a figura.

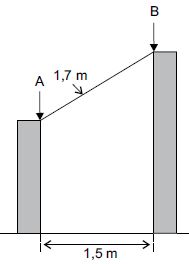
A diferença entre a altura da maior estaca e a altura da menor estaca, nessa ordem, em cm, é:

(A) 95.

(B) 75.

(C) 85.

(D) 80.

(E) 90.

Resolução

Para resolvermos a questão, vamos localizar um triângulo retângulo na figura. Veja:

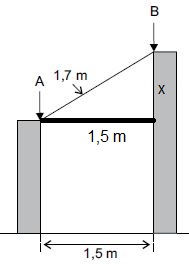
Note que x é exatamente a diferença que queremos, e podemos calculá-lo através do Teorema de Pitágoras:

1,7² = 1,5² + x²

2,89 = 2,25 + x²

x² = 2,89 – 2,25

x² = 0,64

x = 0,8 m ou 80 cm

Gostou da prova resolvida do concurso da Polícia Militar do Estado de São Paulo (PM SP), realizado em 2017 pela Vunesp?

Deixe o seu comentário.