Confira aqui a prova resolvida do Banco do Brasil (BB) de 2023, conteúdo de matemática e matemática financeira, prova A.
MATEMÁTICA
Questão 16. As 2023 assertivas a seguir estão escritas em um caderno.
1) Só 1 assertiva é falsa neste caderno.
2) Só 2 assertivas são falsas neste caderno.
3) Só 3 assertivas são falsas neste caderno. .
.
.
n) Só n assertivas são falsas neste caderno.
.
.
.
2022) Só 2022 assertivas são falsas neste caderno.
2023) Só 2023 assertivas são falsas neste caderno.
Considerando-se essas 2023 assertivas, o número de assertivas verdadeiras é
(A) 2023
(B) 2022
(C) 1011
(D) 1
(E) 0
Resolução
Observe que existem 2023 assertivas, e que cada uma delas menciona um número de assertivas falsas entre 1 e 2023.
Como as assertivas utilizam a palavra “só”, não há como existirem duas ou mais assertivas verdadeiras ao mesmo tempo.
Precisamos descobrir se existem 0 ou 1 assertivas verdadeiras.
Supondo que existem zero assertivas verdadeiras, teríamos que a assertiva de número 2023 é verdadeira, entrando em uma contradição, ou seja, não há como existir zero assertivas verdadeiras.
Conclusão: Existe apenas uma assertiva verdadeira e essa assertiva é a de número 2022, pois se “só 2022 assertivas são falsas”, apenas uma será verdadeira.
Resposta: D
Questão 17. J convenceu o diretor de um curso preparatório a abrir uma turma especialmente para o concurso em que ele pretende se inscrever, e comprometeu-se a trazer mais alunos para formar essa turma. O diretor do curso estabeleceu a seguinte condição:
— Uma sala com 70 lugares, ou seja, com capacidade para até 70 estudantes, será disponibilizada para a turma, desde que cada estudante, incluindo você, J, pague mensalmente R$ 660,00, mais R$ 30,00 por cada lugar vago.
Considerando-se a condição estabelecida pelo diretor, para que o curso tenha arrecadação mensal máxima com essa turma, ela deverá ter exatamente x estudantes. Dividindo-se x por 5, obtém-se resto igual a
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
Resolução
Cada estudante pagará 660 reais mais 30 por lugar vago.
Considere que x representa a quantidade de estudantes matriculados. Como existem 70 lugares disponíveis, a quantidade de lugares vagos será igual a 70-x.
Cada estudante pagará:
660 + 30(70 – x)
660 + 2100 – 30x
2760 – 30x
Como existem x estudantes matriculados, a função que representa o faturamento mensal do curso é:
f(x) = x . (2760 – 30x)
f(x) = 2760x – 30x²
Observe que temos aqui uma função quadrática, onde o coeficiente a<0, ou seja, o gráfico possui o formato de uma parábola com a concavidade para baixo, possuindo um valor máximo.
Colocando 30x em evidência na função, temos:
f(x) = 30x . (92 – x)
Observe que f(x) = 0 quando x = 0 ou x = 92.
O x do vértice pode ser calculado através da média aritmética simples das raízes 0 e 92:
(92 + 0)/2 = 92/2 = 46
Conclusão: O faturamento será máximo quando existirem 46 alunos matriculados.
Dividindo-se 46 por 5, temos como resultado o 9, com resto igual a 1.
Resposta: B
Questão 18. A sequência dos primeiros 2100 números inteiros positivos foi disposta em uma Tabela, da seguinte forma:
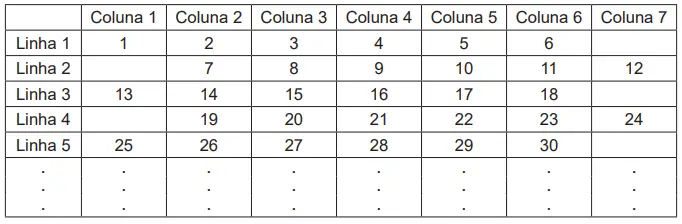
Nessa distribuição, as linhas de número ímpar recebem só seis números da sequência, a partir da Coluna 1, ficando a Coluna 7 vazia; já as linhas de número par também recebem só seis números da sequência, mas a partir da Coluna 2, ficando a Coluna 1 vazia, como pode ser observado na Tabela apresentada.
Sendo assim, os números 1808 e 2023 estão escritos, respectivamente, nas seguintes colunas:
(A) 6 e 4
(B) 3 e 3
(C) 6 e 3
(D) 6 e 2
(E) 3 e 2
Resolução
Devemos observar que sempre aparecem 6 números por linha.
Efetuando-se a divisão de 1808 por 6, temos:
1808 = 301 x 6 + 2 (301, com resto 2)
Observe que existem 301 linhas completas, e que os 2 números restantes estão em uma linha par, ou seja, a coluna 1 ficará vazia, e o número 1808 ficará localizado na coluna 3.
Efetuando-se a divisão de 1808 por 6, temos:
2023 = 337 x 6 + 1 (337, com resto 1)
Observe que existem 337 linhas completas, e que o número restante (2023) está em uma linha par, ou seja, a coluna 1 ficará vazia, e o número 2023 ficará localizado na coluna 2.
Resposta: E
Resolução 19. Três novas agências de um banco estão sendo criadas, e alguns poucos materiais ainda precisam ser comprados. A Tabela a seguir mostra esses materiais e suas respectivas quantidades, pedidas por cada uma dessas agências. Sabe-se que todos os armários são idênticos e têm o mesmo preço, o mesmo ocorrendo com as mesas e com as cadeiras.
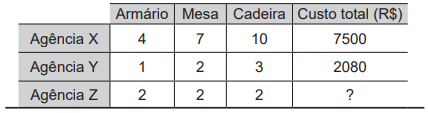
O custo total da compra do material para a Agência Z, em R$, é de
(A) 2.200,00
(B) 2.380,00
(C) 2.460,00
(D) 2.520,00
(E) 2.740,00
Resolução
Considere que:
A = valor de um armário
M = valor de uma mesa
C = valor de uma cadeira
Considerando as informações da agência X, temos:
4A + 7M + 10C = 7500
Considerando as informações da agência Y, temos:
A + 2M + 3C = 2080
Multiplicando a equação por 3:
3A + 6M + 9C = 6240
Subtraindo a equação da agência X pela da agência Y:
4A + 7M + 10C – 3A – 6M – 9C = 7500 – 6240
A + M + C = 1260
Observe que precisamos calcular o custo da agência Z, ou seja, quanto é 2A + 2M + 2C. Observando a equação anterior, podemos multiplicá-la por 2:
2.(A + M + C = 1260) = 2A + 2M + 2C = 2520
Resposta: D
Questão 20. Um investidor muito supersticioso escolhe, mensalmente, um conjunto de três tipos de investimento para aplicar alguma quantia. Ele toma por regra dispor apenas dos mesmos nove tipos de investimentos e nunca repetir, em um mesmo mês, o mesmo conjunto de três tipos já usados em qualquer mês anterior. Por exemplo, se no 1o mês ele escolheu os investimentos de tipos A, B e C; no 2o mês, A, B e D; e no 3o mês, E, F e G, então ele não poderá investir novamente, num mesmo mês, por exemplo, no conjunto dos investimentos de tipos A, B e C, por já tê-lo usado no 1o mês.
Considerando-se as condições descritas, o número máximo de meses em que o investidor poderá fazer esses investimentos é
(A) 84
(B) 60
(C) 56
(D) 48
(E) 35
Resolução
Observe que ele sempre escolhe 3 entre 9 opções, e que a ordem da escolha é irrelevante, ou seja, temos uma combinação de 9, tomados 3 a 3.
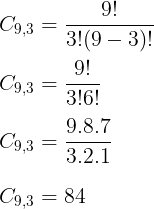
Resposta: A
PROVA RESOLVIDA BB 2023 – MATEMÁTICA FINANCEIRA – PROVA A
Questão 26. Um cliente tem duas opções para investir R$ 100.000,00 em um prazo de 2 anos. A primeira opção oferece um retorno de 12% ao ano no regime de juros compostos, mas há cobrança de 15% de imposto sobre os juros proporcionados pelo investimento. Já a segunda opção oferece um retorno de 10% ao ano no regime de juros compostos, mas sem qualquer cobrança de imposto. Ao escolher a opção mais lucrativa, ao final de exatos dois anos de investimento, esse cliente receberá a mais, em relação à opção menos lucrativa, uma quantia, em R$, igual a
(A) 624,00
(B) 824,00
(C) 1.524,00
(D) 2.940,00
(E) 4.440,00
Resolução
Opção 1:
M = C . (1 + i)n
M = 100000 . (1 + 0,12)2
M = 100000 . 1,122
M = 100000 . 1,2544
M = 125440
Imposto de Renda sobre o rendimento de 25440:
25440 x 15% = 3816
25440 – 3816 = 21624
Valor após cobrança de IR: R$ 121.624,00
Opção 2:
M = C . (1 + i)n
M = 100000 . (1 + 0,1)2
M = 100000 . 1,12
M = 100000 . 1,21
M = R$ 121.000,00
Diferença:
121624 – 121000 = R$ 624,00
Resposta: A
Questão 27. Um banco oferece para um cliente um investimento que lhe proporcionará uma taxa de juros de 1% ao mês, no regime de juros compostos. Esse mesmo banco também disponibiliza, para o mesmo cliente, uma linha de crédito de fácil acesso chamada cheque especial, cobrando uma taxa de juros de 4% ao mês, no regime de juros compostos. Para esse cliente, a diferença entre a taxa anual da operação financeira disponível no cheque especial e a taxa anual da operação financeira disponível no investimento oferecido é

(A) 12,68%
(B) 36,00%
(C) 47,42%
(D) 48,68%
(E) 60,10%
Resolução
Calcularemos a taxa anual em ambos os casos, onde consideraremos que o capital é igual a 1.
Investimento
M = C . (1 + i)n
M = 1 . (1 + 0,01)12
M = 1,0112
M = 1,1268
Taxa anual de 12,68% a.a.
Cheque Especial
M = C . (1 + i)n
M = 1 . (1 + 0,04)12
M = 1,0412
M = 1,6010
Taxa anual de 60,10% a.a.
Diferença:
60,10 – 12,68 = 47,42%
Resposta: C
Questão 28. O capital de um cliente do segmento ultra-especial ficou aplicado durante 50 dias a uma taxa de juros simples de 1,5% ao mês. Ao final desse prazo, o cliente resgatou tudo e pagou R$ 4.500,00, referentes a 22,5% de imposto de renda sobre os juros proporcionados pelo investimento.
Considerando-se o mês com 30 dias, o valor aplicado nessa operação, em R$, foi
(A) 450.000,00
(B) 700.000,00
(C) 750.000,00
(D) 800.000,00
(E) 950.000,00
Resolução
Considerando que o cliente pagou 4500 de imposto de renda, e que a alíquota é de 22,5%, podemos calcular o total (J) dos juros proporcionados pelo investimento:
J . 22,5% = 4500
J = 4500 / 0,225
J = 20000
Agora que sabemos os juros gerados, considerando ainda que a taxa de juros simples é de 1,5% a.m., por um prazo de 50 dias, temos que:
J = M . 1,5% . (50/30)
20000 = M . 0,015 . 5/3
20000 = M . 0,025
M = 20000 / 0,025
M = R$ 800.000,00
Resposta: D
Questão 29. A empresa XYZ planeja comprar um equipamento em janeiro de 2023, cujo preço à vista é R$ 300.000,00, pagando com uma entrada e mais duas parcelas. A entrada, correspondente à primeira parcela, será paga em janeiro de 2023 (no ato da compra); a segunda parcela, em janeiro de 2024, no valor de R$ 150.000,00; e a terceira parcela, em janeiro de 2025, também no valor de R$ 150.000,00.
Considerando-se a equivalência financeira a juros compostos, se a taxa de juros cobrada pelo vendedor é de 10% ao ano, o valor da entrada (primeira parcela no ato da compra), em R$, será, aproximadamente,
(A) 20.000,00
(B) 39.670,00
(C) 48.750,00
(D) 54.280,00
(E) 63.000,00
Resolução
Faremos a descapitalização das duas últimas prestações, considerando a taxa de juros de 10% a.a..
Segunda parcela:
150000 / 1,1 = 136.363,63
Terceira parcela:
150000 / 1,12 = 123.966,94
Total das duas últimas parcelas descapitalizadas:
136363,63 + 123966,94 = R$ 260.330,57
Valor da entrada:
300000 – 260330,57 = R$ 39.669,43
Resposta: B
Questão 30. Uma empresa tomou um empréstimo de R$ 50.000,00 em janeiro de 2022, a uma taxa de juros compostos de 5% ao mês. Para amortizar parte da dívida, a empresa pagou R$ 30.000,00 em março de 2022, e R$ 20.000,00 em abril de 2022.
No que se refere a esse empréstimo, o valor, em R$, do saldo devedor dessa empresa, em maio de 2022, era, aproximadamente,
(A) 3.625,00
(B) 3.806,00
(C) 6.381,00
(D) 6.700,00
(E) 7.201,00
Resolução
Calcularemos a evolução da dívida mensalmente:
Fevereiro, após 1 mês da contratação.
Saldo devedor: 50000 x 1,05 = 52.500
Março
Saldo devedor: 52500 x 1,05 = 55125
Após pagamento de 30 mil: 55125 – 30000 = 25125
Abril
Saldo devedor: 25125 x 1,05 = 26381,25
Após pagamento de 20 mil: 26381,25 – 20000 = 6381,25
Maio
Saldo devedor: 6381,25 x 1,05 = 6700
Resposta: D
Gostou da prova resolvida do concurso para o BB de 2023? Deixe o seu comentário.
