Confira a prova resolvida do concurso para Guarda Civil do Estado de São Paulo (SP) realizado em 2010.
16. Marta mora com Pedro, seu esposo, e seus dois filhos, Luiza e Thiago. Ela foi ao supermercado e comprou alimentos suficientes para o consumo de sua família por 15 dias. No entanto, inesperadamente, duas tias vieram visitá-la e se hospedaram em sua casa durante esse período. Supondo que todos se alimentem com quantidades iguais, em quanto tempo os alimentos acabarão?
a) 22,5 dias.
b) 15 dias.
c) 12 dias.
d) 10 dias.
e) 8 dias.
A quantidade de comida é suficiente para 4 pessoas durante 15 dias.
Se aumentarmos para 6 pessoas, a comida certamente durará menos que 15 dias (grandezas inversamente proporcionais).
Regra de três:
17. Em uma fábrica de roupas, 10 costureiras, trabalhando em um mesmo ritmo, fabricam 50 shorts em 1 hora. Em quanto tempo 8 costureiras, trabalhando nesse mesmo ritmo, fabricam 40 shorts?
a) 1 hora.
b) 30 minutos.
c) 2 horas.
d) 2 horas e 30 minutos.
e) 3 horas.
Regra de três composta:
Quanto mais horas, menos costureiras são necessárias (inversamente proporcionais)
Quanto mais horas, mais shorts são feitos (diretamente proporcionais)
18. Um carro, a uma velocidade média de 110 km/h, percorre uma certa distância em 2 horas e 30 minutos. Se a velocidade média fosse de 90 km/h, o tempo gasto para percorrer essa mesma distância seria de aproximadamente:
a) 3,5 horas.
b) 3 horas.
c) 2 horas.
d) 2,5 horas.
e) 4 horas.
Percorrendo 2 horas e 30 minutos (2,5 horas) a velocidade média de 110 km/h ele percorre:
110.2,5 = 275 km
Se a velocidade média fosse 90km/h:
275km / 90km/h = 275/90 = 3,05 (aproximadamente 3 horas)
19. Em uma escola, 25% dos alunos estão no ensino médio. Desses, 30% estão no primeiro ano e 40% no segundo ano. Sabendo que 60% dos alunos do terceiro ano passaram no vestibular e que a escola possui 400 alunos no ensino médio, quantos alunos passaram no vestibular?
a) 60.
b) 12.
c) 22.
d) 30.
e) 18.
Se 30% estão no primeiro ano e 40% no segundo ano, 30% estão no terceiro ano, que possui:
400.30% = 400.30/100 = 12000/100 = 120 alunos
Como 60% passaram:
120.60% = 72 alunos
Questão anulada pois não existe a resposta no gabarito.
20. Para vender todas as frutas que restavam, um feirante fez a seguinte promoção: Leve 4 e pague 3. Vendo a promoção do colega ao lado, um outro feirante anunciou: Leve 5 e pague 4. Sabendo que os dois feirantes vendem as frutas pelo mesmo preço, quais são os percentuais de desconto oferecidos, respectivamente?
a) 33% e 18%
b) 40% e 50%
c) 25% e 20%
d) 10% e 10%
e) 14% e 18%
Leve 4 e pague 3: O cliente está comprando 4 e ganhando uma de brinde. 1/4 = 25%
Leve 5 e pague 4: O cliente está comprando 5 e ganhando uma de brinde. 1/5 = 20%
21. O resto da divisão do polinômio x³ + 3x² – 5x + 1 por x – 2 é:
a) 1
b) 2
c) 10
d) 11
e) 12
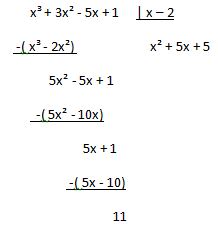
22. Considere o polinômio
Sabendo que P(1) = 2, então o valor de P(3) é:
a) 386.
b) 405.
c) 324.
d) 81.
e) 368.
P(1)=4.1 + 3.1 – 2.1 + 1 + k =2
4 + 3 – 2 + 1+ k = 2
10 + k = 2
k = 2 – 6
k = – 4
O polinômio será P(x) = 4x^4 + 3x³ + 2x² + x – 4
P(3) = 4x^4 + 3x³ + 2x² + x – 4
= 4.81 + 3.27 – 2.9 + 3 – 4
= 324 + 81 – 18 + 3 – 4
= 386
23. A soma entre dois números positivos é 37. Se o produto entre eles é 330, então o valor da diferença entre o maior e o menor número é:
a) 7.
b) 23.
c) 61.
d) 17.
e) 49.
Sejam x e y esses números:
x + y = 37
x.y = 330
Da primeira equação temos que y = 37 – x, que substituindo na segunda:
x(37 – x) = 330
37x – x² – 330 = 0
x² – 37x + 330 = 0
Note que a = 1, b = -37, c = 330
Calculando o valor de Δ:
Δ = b² – 4ac = (-37)² – 4.1.(330) = 1369 – 1320 = 49
Calculando as raízes:
Daí, x’ = (37+7)/2 = 22 e x” = (37-7)/2 = 15
Assim, se x = 22, y = 15, e se x = 15, y = 22.
Logo, 22 – 15 = 7
24. Se x1 > x2 são as raízes da equação x² – 27x + 182 = 0, então o valor de 1/x2 – 1/x1 é:
a) 1/27
b) 1/13
c) 1
d) 1/182
e) 1/14
Note que a = 1, b = -27, c = 182
Calculando o valor de Δ:
Δ = b² – 4ac = (-27)² – 4.1.(182) = 729 – 728 = 1
Calculando as raízes:
Daí, x’ = (27+1)/2 = 14 e x” = (27-1)/2 = 13
Logo,
1/13 – 1/14 = (14 – 13)/182 = 1/182
25. Marcos pagou sua conta de energia no valor de R$ 240,00 com notas de R$ 5,00 e R$ 20,00. Sabendo que ele usou 30 notas ao todo, quantas notas havia de cada valor?
a) 23 notas de R$ 5,00 e 7 notas de R$ 20,00.
b) 24 notas de R$ 5,00 e 6 notas de R$ 20,00.
c) 22 notas de R$ 5,00 e 8 notas de R$ 20,00.
d) 18 notas de R$ 5,00 e 12 notas de R$ 20,00.
e) 20 notas de R$ 5,00 e 10 notas de R$ 20,00.
x = quantidade de notas de 5 reais
y = quantidade de notas de 20 reais
(1) 5x + 20y = 240 (Simplificando temos: x + 4y = 48)
(2) x + y = 30
Fazendo (1) – (2):
x + 4y – x – y = 48 – 30
3y = 18
y = 18/3
y = 6
De x + y = 30, temos que x = 24
26. A soma entre quatro números pares consecutivos é 116. Quais são esses números?
a) 18, 20, 22 e 24.
b) 20, 22, 24 e 26.
c) 28, 30, 32 e 34.
d) 24, 26, 28 e 30.
e) 26, 28, 30 e 32.
Vamos considerar os quatro pares consecutivos como: 2k, 2k + 2, 2k + 4, 2k + 6
2k + 2k + 2 + 2k + 4 + 2k + 6 = 116
8k + 12 = 116
8k = 116 – 12
8k = 104
k = 104/8
k = 13
Logo, os números serão: 26, 28, 30 e 32
27. O valor de x na equação 2x/3 – x/5 = 6(x – 2) é:
a) 160/73
b) 120/53
c) 180/83
d) 140/63
e) 100/43
2x/3 – x/5 = 6(x – 2)
(5.2x – 3.x)/15 = 6(x – 2)
10x – 3x = 90(x – 2)
7x = 90x – 180
180 = 90x – 7x
83 x = 180
x = 180/83
28. Qual o valor da expressão √(0,0016) : √(0,000064) ?
a) 0,0005
b) 0,005
c) 0,5
d) 5
e) 50
√(0,0016) = √(16/10000) = 4/100 =
√(0,000064) = √(64/1000000) = 8/1000
29. Anulada
30. Qual o valor de x na expressão abaixo?
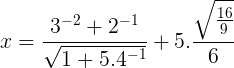
a) 1/27
b) 41/27
c) 1/17
d) 11/18
e) 41/17
Vamos calcular por partes:
3-² + 2-¹ = 1/9 + 1/2 = (2 + 9)/18 = 11/18
√(1 + 5.4-¹) = √(1 + 5/4) = √[(4 + 5)/4] = √(9/4) = 3/2
5.√(16/9)/6 = 5.(4/3)/6 = 5.4/6.3 = 20/18 = 10/9
(11/18) / (3/2) = 11.2/18.3 = 22/54 = 11/27
11/27 + 10/9 = (11 + 30)/27 = 41/27