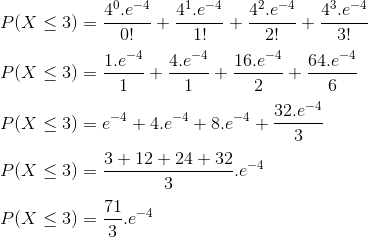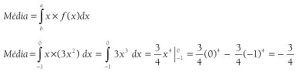Confira aqui a prova resolvida e comentada do concurso de auditor da Receita Federal do Brasil (RFB), realizado em 2009 pela ESAF.
Não deixe de ver em nossa menu outras provas resolvidas sobre este e outros concursos.
Bom estudo!
Questão 31. Considere a seguinte proposição: “Se chove ou neva, então o chão fica molhado”. Sendo assim, pode-se afirmar que:
a) Se o chão está molhado, então choveu ou nevou.
b) Se o chão está molhado, então choveu e nevou.
c) Se o chão está seco, então choveu ou nevou.
d) Se o chão está seco, então não choveu ou não nevou.
e) Se o chão está seco, então não choveu e não nevou.
Resolução
Temos 3 proposições:
P = Chove
Q = Neva
R = Chão molhado
Podemos escrever a proposição “Se chove ou neva, então o chão fica molhado” como P∨Q ⇒ R, que é equivalente a ~R ⇒ ~P∧~Q, ou seja, “Se o chão está seco, então não choveu e não nevou”
Resposta: E
Questão 32. Três meninos, Zezé, Zozó e Zuzu, todos vizinhos, moram na mesma rua em três casas contíguas. Todos os três meninos possuem animais de estimação de raças diferentes e de cores também diferentes. Sabe-se que o cão mora em uma casa contígua à casa de Zozó; a calopsita é amarela; Zezé tem um animal de duas cores – branco e laranja – ; a cobra vive na casa do meio. Assim, os animais de estimação de Zezé, Zozó e Zuzu são, respectivamente:
a) cão, cobra, calopsita.
b) cão, calopsita, cobra.
c) calopsita, cão, cobra.
d) calopsita, cobra, cão.
e) cobra, cão, calopsita.
Resolução
De “o cão mora em uma casa contígua à casa de Zozó”, temos que o cão não pertence a Zozó. Descartamos então as alternativas C e E.
De “a calopsita é amarela” e “Zezé tem um animal de duas cores – branco e laranja”, temos que a calopsita não pertence a Zezé. Descartamos então as questões C e D.
Restaram as alternativas A e B, daí podemos concluir que Zezé possui um cão, e de “Zezé tem um animal de duas cores – branco e laranja”, que o cão é branco e laranja.
De “a cobra vive na casa do meio” e “o cão mora em uma casa contígua à casa de Zozó”, a cobra só pode pertencer a Zozó.
Resposta: A

Resolução
Vamos reescrever o exercício da seguinte forma:
Se alfa tem raiz, então beta tem raiz. Se alfa tem potência, então beta ou delta tem raiz. Se delta tem potência, então beta tem potência. Se delta tem raiz, então alfa tem raiz.
A alternativa “a” é descartada pela proposição “Se alfa tem potência, então beta ou delta tem raiz”
A alternativa “b” é descartada pela proposição “Se delta tem raiz, então alfa tem raiz”
As alternativas “c” e “e” são descartadas pela proposição “Se alfa tem raiz, então beta tem raiz”
Note que a alternativa “d” não é contrária a nenhuma das proposições.
Resposta: D

Resolução
Vamos calcular as raízes de f(x):
Δ = b² – 4.a.c = (-2)² – 4.1.1 = 4 – 4 = 0
x = (-b +- √Δ)/2a = (2 +- 0)/2 = 2/2 = 1
Como o gráfico de uma função do segundo grau é uma parábola, f(x) só tem uma raíz igual a 1 e a>0, temos uma parábola com o “buraco” para cima e o vértice no ponto (1,0). Logo, f(x) é menor ou igual a zero apenas quando x=1.
Logo A = {1}.
Como não temos a opção de Y ser vazio, só nos resta a alternativa C.
Questão 35. Em uma repartição, 3/5 do total dos funcionários são concursados, 1/3 do total dos funcionários são mulheres e as mulheres concursadas correspondem a 1/4 do total dos funcionários dessa repartição. Assim, qual entre as opções abaixo, é o valor mais próximo da porcentagem do total dos funcionários dessa repartição que são homens não concursados?
a) 21%
b) 19%
c) 42%
d) 56%
e) 32%
De “3/5 do total dos funcionários são concursados” temos que 60% são concursados e 40% não são concursados.
De “mulheres concursadas correspondem a 1/4 do total dos funcionários” temos que 25% dos funcionários são mulheres concursadas.
De “1/3 do total dos funcionários são mulheres” temos que as mulheres correspondem a aproximadamente 33%.
Daí, a porcentagem de mulheres não concursadas é 33 – 25 = 8%.
Como 40% dos funcionários não são concursados, a porcentagem de homens não concursados é 40 – 8 = 32%
Questão 36. Um projétil é lançado com um ângulo de 30º em relação a um plano horizontal. Considerando que a sua trajetória inicial pode ser aproximada por uma linha reta e que sua velocidade média, nos cinco primeiros segundos, é de 900km/h, a que altura em relação ao ponto de lançamento este projétil estará exatamente cinco segundos após o lançamento?
a) 0,333 km
b) 0,625 km
c) 0,5 km
d) 1,3 km
e) 1 km
Como ele tem velocidade média de 900km/h, e uma hora possui 3600 segundos, temos que a velocidade em km/seg é de 900/3600 = 0,25 km/seg. Como queremos saber a distância após 5 segundos, ele viajou 0,25 x 5 = 1,25 km.
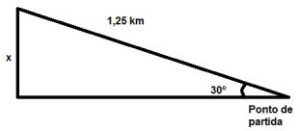
Observe o triângulo que representa a trajetória do projétil. Desejamos descobrir a altura, ou seja, o valor de x.
Temos que sen30º = cateto oposto / hipotenuza
0,5 = x / 1,25
x = 1,25 . 0,5 = 0,625 km

Podemos separar a segunda igualdade em duas:
2x – y = 3z + 2 => 2x – y – 3z = 2
2x + y = z + 1 => 2x + y – z = 1
Temos então três equações:
x + y + z = 1
2x – y – 3z = 2
2x + y – z = 1
Que podem ser associadas a matriz:
| 1 1 1 |
| 2 -1 -3 |
| 2 1 -1 |
Vamos calcular seu determinante:
| 1 1 1 | 1 1
| 2 -1 -3 | 2 -1
| 2 1 -1 | 2 1
Det = 1.(-1).(-1) + 1.(-3).2 + 1.2.1 – 2.(-1).1 – 1.(-3).1 – (-1).2.1 = 1 – 6 + 2 +2 + 3 + 2 = 4
Questão 38. Considere uma esfera, um cone, um cubo e uma pirâmide. A esfera mais o cubo pesam o mesmo que o cone. A esfera pesa o mesmo que o cubo mais a pirâmide. Considerando ainda que dois cones pesariam o mesmo que três pirâmides, quantos cubos pesa a esfera?
a) 4
b) 5
c) 3
d) 2
e) 1
Vamos denominar:
A = volume da esfera
B = volume do cubo
C = volume do cone
D = volume da piramide
(1) A esfera mais o cubo pesam o mesmo que o cone: A + B = C
(2) A esfera pesa o mesmo que o cubo mais a pirâmide: A = B + D => A – B = D
(3) Dois cones pesariam o mesmo que três pirâmides: 2C = 3D => D = 2C/3
Substituindo (3) em (2):
(4) A – B = 2C/3
Multiplicando (1) por 2/3:
(5) 2A/3 + 2B/3 = 2C/3
Fazendo (4) – (5):
A – 2A/3 – B -2B/3 = 2C/3 – 2C/3
A/3 – 5B/3 = 0
A/3 = 5B/3
A = 5B
Questão 39. Se um polinômio f for divisível separadamente por (x – a) e (x – b) com a ≠ b, então f é divisível pelo produto entre (x–a) e (x–b). Sabendo-se que 5 e -2 são os restos da divisão de um polinômio f por (x – 1) e (x + 3), respectivamente, então o resto da divisão desse polinômio pelo produto dado por (x – 1) e (x + 3) é igual a:
a) 13x/4 + 7/4
b) 7x/4 – 13/4
c) 7x/4 + 13/4
d) -13x/4 – 13/4
e) -13x/4 – 7/4
Primeiramente, o resto da divisão de um polinômio P(x) por (x-a) é igual a P(a)
Dividindo o polinômio f pelo polinômio de grau 2, resultado do produto (x-1).(x+3). Observe que o resto deve ter grau 1 ou 0 (se divisão exata). Vamos chamar o resto de ax + b.
Temos::
P(1) = 5 (5 é o resto da divisão de f por x-1)
P(-3) = -2 (-2 é o resto da divisão de f por x+3)
Daí,
a.1 + b = 5
a.(-3) + b = -2
Subtraindo a equação 1 pela equação 2, temos:
4a = 7
a = 7/4
Substituindo “a” na equação 1, temos:
7/4 + b = 5
b = 5 – 7/4
b = 13/4
Concluímos que o resto é ax + b = (7/4).x + 13/4
Questão 40. Sabe-se que os pontos A,B,C, D, E, F e G são coplanares, ou seja, estão localizados no mesmo plano. Sabe-se, também, que destes sete pontos, quatro são colineares, ou seja, estão numa mesma reta. Assim, o número de retas que ficam determinadas por estes sete pontos é igual a:
a) 16
b) 28
c) 15
d) 24
e) 32
Resolução 1: Temos que dois pontos bastam para determinar uma reta, então basta fazer a combinação dos 7 pontos tomados 2 a 2, subtraindo a combinação dos 4 pontos (colineares) tomados 2 a 2, somando a reta que passa pelos 4 pontos colineares.
C7,2 – C4,2 + 1 = 7!/(7-2)!2! – 4!/(4-2)!2! + 1 = 21 – 6 + 1 = 16
Resolução 2:
Vamos analisar da seguinte forma:
Cada um dos 3 pontos não colineares pode ser ligado nos 4 pontos colineares, ou seja, cada um forma 4 retas, daí, temos 3×4 = 12 retas.
Podemos também formar 3 retas utilizando apenas os 3 pontos não colineares.
Por último, uma reta que passa pelos 4 pontos colineares.
Logo, 12 + 3 + 1 = 16
Questão 41. ANULADA
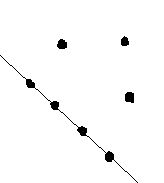
Questão 42. Considere um retângulo formado por pequenos quadrados iguais, conforme a figura abaixo. Ao todo, quantos quadrados de quaisquer tamanhos podem ser contados nessa figura?
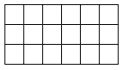
a) 128
b) 100
c) 64
d) 32
e) 18
Podemos formar 18 quadrados 1×1, 10 quadrados 2×2 e 4 quadrados 3×3.
18+10+4 = 32
Questão 43. Considere a seguinte amostra aleatória das idades em anos completos dos alunos em um curso preparatório. Com relação a essa amostra, marque a única opção correta:
29, 27, 25, 39, 29, 27, 41, 31, 25, 33, 27, 25, 25, 23, 27, 27, 32, 26, 24, 36, 32, 26, 28, 24, 28, 27, 24, 26, 30, 26, 35, 26, 28, 34, 29, 23, 28.
a) A média e a mediana das idades são iguais a 27.
b) A moda e a média das idades são iguais a 27.
c) A mediana das idades é 27 e a média é 26,08.
d) A média das idades é 27 e o desvio-padrão é 1,074.
e) A moda e a mediana das idades são iguais a 27.
Primeiramente vamos colocar as 37 idades em ordem crescente:
23, 23, 24, 24, 24, 25, 25, 25, 25, 26, 26, 26, 26, 26, 27, 27, 27, 27, 27, 27, 28, 28, 28, 28, 29, 29, 29, 30, 31, 32, 32, 33, 34, 35, 36, 39, 41.
A moda é o valor que aparece com mais frequência. Note que o 27 aparece 6 vezes e nenhum outro aparece com tanta frequência.
A mediana é o valor que, após ordenar todos os valores, se encontra no centro. Note que o 27 se encontra na posição 19º, ou seja, exatamente no meio.
Questão 44. ANULADA
Questão 45. O número de petroleiros que chegam a uma refinaria ocorre segundo uma distribuição de Poisson, com média de dois petroleiros por dia. Desse modo, a probabilidade de a refinaria receber no máximo três petroleiros em dois dias é igual a:
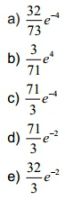
Resolução
Veja abaixo a fórmula para se determinar a probabilidade de um dado número X de sucessos em uma distribuição de Poisson. Onde e = 2,71828… é a constante de Euler.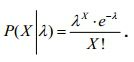 A média é de dois petroleiros por dia. Obviamente, a cada dois dias, teremos uma média de 4 petroleiros, logo λ=4.
A média é de dois petroleiros por dia. Obviamente, a cada dois dias, teremos uma média de 4 petroleiros, logo λ=4.
Calculando a probabilidade da plataforma receber no máximo 3 petroleiros em 2 dias:
P(X≤3) = P(X=0) + P(X=1) + P(X=2) + P(X=3)
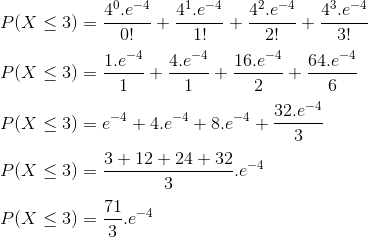
Resposta: C
Questão 46. Em um experimento binomial com três provas, a probabilidade de ocorrerem dois sucessos é doze vezes a probabilidade de ocorrerem três sucessos. Desse modo, as probabilidades de sucesso e fracasso são, em percentuais, respectivamente, iguais a:
a) 80 % e 20 %
b) 30 % e 70 %
c) 60 % e 40 %
d) 20 % e 80 %
e) 25 % e 75 %
Sejam p e q as probabilidades de sucesso e fracasso respectivamente.
C3,2.p².q = 12.C3,3.p³
Então,
3.p².q = 12.1.p³
q = 4p (I)
De p e q complementares:
p + q = 1 (II)
Substituíndo I em II:
p + (4p) = 1, ou seja, 5p = 1
p = 1/5.
Note que 1/5 representa 20%. Temos assim que q deve ser 80%.
Questão 47. A função densidade de probabilidade de uma variável aleatória contínua x é dada por:
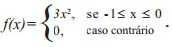
Para esta função, a média de x, também denominada expectância de x e denotada por E(x) é igual a:
a) 4/3
b) 3/4
c) -3/4
d) -3x/4
e) -4x/3
Podemos achar a resposta por eliminação:
Podemos eliminar as alternativas ‘a’ e ‘b’ pois a média pertence a um intervalo negativo.
Podemos eliminar as alternativas ‘d’ e ‘e’ pois estão em função de x, isso não é média.
Resolução:
Podemos resolver utilizando a fórmula da integral:
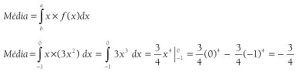
Questão 48. A tabela mostra a distribuição de frequências relativas populacionais (f’) de uma variável X:
Questão 49. No sistema de juros compostos um capital PV aplicado durante um ano à taxa de 10 % ao ano com capitalização semestral resulta no valor final FV. Por outro lado, o mesmo capital PV, aplicado durante um trimestre à taxa de it % ao trimestre resultará no mesmo valor final FV, se a taxa de aplicação trimestral for igual a:
a) 26,25 %
b) 40 %
c) 13,12 %
d) 10,25 %
e) 20 %
Resolução:
Primeiro Caso: FV = PV. (1+5%)²
Segundo Caso: FV = PV. (1+it%)
Igualando:
PV.(1+5%)² = PV. (1+it%)
PV.(1 + 0,05)² = PV. (1+it%)
(1,05)² = (1+it%)
1,1025 = 1+it
it = 0,1025
it = 10,25%
Questão 50. Um corredor está treinando diariamente para correr a maratona em uma competição, sendo que a cada domingo ele corre a distância da maratona em treinamento e assim observou que, a cada domingo, o seu tempo diminui exatamente 10% em relação ao tempo do domingo anterior. Dado que no primeiro domingo imediatamente antes do início do treinamento, ele fez o percurso em 4 horas e 30 minutos e, no último domingo de treinamento, ele correu a distância da maratona em 3 horas, 16 minutos e 49,8 segundos, por quantas semanas ele treinou?
a) 1
b) 5
c) 2
d) 4
e) 3
Note que:
4 horas e 30 minutos = 16200 segundos
3 horas, 16 minutos e 49,8 segundos = 11809,8 segundos
Reduzir 10% significa multiplicar por 0,9.
Assim,
(0,9)^n = 11809,8 / 16200
(0,9)^n = 0,729
(0,9)^n = (0,9)^3
n = 3
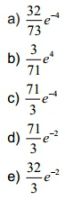
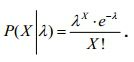 A média é de dois petroleiros por dia. Obviamente, a cada dois dias, teremos uma média de 4 petroleiros, logo λ=4.
A média é de dois petroleiros por dia. Obviamente, a cada dois dias, teremos uma média de 4 petroleiros, logo λ=4.