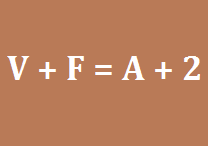Confira aqui a fórmula matemática conhecida como a Relação de Euler, onde apresentaremos a definição, quando e como utilizá-la.
Trata-se do estudo dos poliedros, matéria da matemática espacial. Vale a pena conferir.
Bom estudo!
A Relação de Euler é uma importante ferramenta para relacionar o número de vértices, arestas e faces de um poliedro convexo. Assim, para todo poliedro convexo, temos que:
V + F = A + 2
Onde:
V = número de vértices do poliedro
F = número de faces do poliedro
A = número de arestas do poliedro
Utilizar a Relação de Euler é bem simples. Vamos verificá-la para alguns exemplos conhecidos:
EXEMPLO 1. Verificar a Relação de Euler para o cubo.
Analisando a figura, temos que:
V = 8
F = 6
A = 12
Verificando a fórmula matemática:
V + F = A + 2
8 + 6 = 12 + 2
14 = 14
EXEMPLO 2. Verificar a Relação de Euler para a pirâmide quadrangular.
Analisando a figura, temos que:
V = 5
F = 5
A = 8
Verificando a fórmula matemática:
V + F = A + 2
5 + 5 = 8 + 2
10 = 10
EXEMPLO 3. Verificar a Relação de Euler para o poliedro convexo abaixo.
Analisando a figura, temos que:
V = 8
F = 6
A = 12
Verificando a fórmula matemática:
V + F = A + 2
8 + 6 = 12 + 2
14 = 14
EXEMPLO 4. Quantas arestas e quantos vértices tem um poliedro convexo de 20 faces triangulares?
A fórmula relaciona arestas, vértices e faces. Como já sabemos a quantidade de faces, precisamos descobrir a quantidade de arestas ou de vértices para utilizarmos a Relação de Euler.
Como são 20 faces triangulares, podemos descobrir a quantidade de arestas multiplicando 20 x 3 = 60, e dividindo por dois, pois em nosso cálculo a mesma aresta foi contada duas vezes. Assim, temos 30 arestas.
Utilizando a fórmula:
V + F = A + 2
V + 20 = 30 + 2
V = 32 – 20
V = 12
Daí, o poliedro possui 30 arestas e 12 vértices.