Buscando exercícios resolvidos sobre média, moda e mediana? Aqui você encontra questões de concursos públicos realizados por todo o país, de diversas bancas e níveis.
Os concursos que exigem dos inscritos conhecimento sobre estatística de nível superior estão entre os mais difíceis e concorridos. Por isso é muito importante dominar os conteúdos introdutórios como média, moda e mediana.
Comece já a estudar e saia na frente.
Bons estudos!
Questão 1 (TJ SP 2014 – Vunesp). Certa competição tem 6 etapas eliminatórias. Sabe-se que a média aritmética do número de pessoas que participaram da primeira e da segunda etapa é igual ao quádruplo da média aritmética do número de pessoas que participaram de cada uma das quatro etapas seguintes.
Desse modo, a razão entre o número de pessoas que participaram da primeira e da segunda etapa e o número total de pessoas que participaram dessa competição é de
a) 1/2
b) 1/3
c) 1/4
d) 2/3
e) 3/4
Resolução:
Vamos representar cada etapa pelas letras a, b, c, d, e, f, nesta ordem.
Utilizando o conceito de média aritmética, temos pelo enunciado que:
(a + b)/2 = 4.(c + d + e + f)/4
(a + b)/2 = (c + d + e + f)
Somando (a + b) em ambos os lados temos:
(a + b)/2 + (a + b) = (c + d + e + f) + (a + b)
(a + b)/2 + 2(a + b)/2 = (a + b + c + d + e + f)
(a + b)3/2 = (a + b + c + d + e + f)
(a + b) = (a + b + c + d + e + f)2/3
Logo, a quantidade de participantes das duas primeiras etapas representa 2/3 do total.
Resposta: D
Clique aqui para assistir a resolução no youtube.
Questão 2 (BB 2013 – Fundação Carlos Chagas). Nos quatro primeiros dias úteis de uma semana o gerente de uma agência bancária atendeu 19, 15, 17 e 21 clientes. No quinto dia útil dessa semana esse gerente atendeu n clientes. Se a média do número diário de clientes atendidos por esse gerente nos cinco dias úteis dessa semana foi 19, a mediana foi
(A) 21.
(B) 19.
(C) 18.
(D) 20.
(E) 23.
Resolução:
Para calcularmos a média aritmética, somamos os valores e dividimos pela quantidade de termos:
Média = (19 + 15 + 17 + 21 + n) / 5 = 19
19 + 15 + 17 + 21 + n = 19 x 5
72 + n = 95
n= 95 – 72 = 23
Nossa sequencia ordenada é então: 15, 17, 19, 21, 23
Como a mediana é o termo do meio quando ordenados, a resposta é 19.
Resposta: B
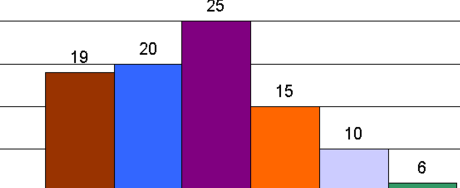
Questão 3 (PM ES 2013 – Exatus). A tabela que segue é demonstrativa do levantamento realizado por determinado batalhão de Polícia Militar, no que se refere às idades dos policiais integrantes do grupo especial desse batalhão:
Idade Nr. de Policiais
25 12
28 15
30 25
33 15
35 10
40 8
A moda, média e mediana dessa distribuição são, respectivamente, iguais a:
a) 30, 31, 30
b) 30, 31, 31
c) 30, 30, 31
d) 31, 30, 31
e) 31, 31, 30
Resolução:
Moda é o valor que aparece com mais frequência: 30.
Média: Temos que somar todas as idades e dividir pela quantidade de policiais:
(25×12 + 28×15 + 30×25 + 33×15 + 35×10 + 40×8)/85
= (300 + 420 + 750 + 495 + 350 + 320)/85
= 2635/85 = 31
Mediana é o termo do meio quando colocamos todos em ordem:
São 85 termos, o do meio é o termo de número 43, ou seja, 30 anos.
Resposta: A
Questão 4 (Prova Resolvida PM ES 2013 – Funcab). A tabela abaixo representa os dados dos balanços das operações do Batalhão de Polícia de Trânsito (BPTran) da Polícia Militar – ES em três grandes feriados nacionais do ano de 2012.
Dia do trabalho: 220 acidentes, 2 mortos, 78 feridos
Dia de finados: 186 acidentes, 2 mortos, 54 feridos
Dia do trabalho: 219 acidentes, 1 mortos, 51 feridos
O valor que melhor representa a média do número de feridos, de acordo com a tabela acima, é:
A) 57
B) 59
C) 61
D) 63
E) 65
Resolução:
Calculando a média aritmética:
(78 + 54 + 51)/3 = 183/3 = 61
Resposta: C
Questão 5 (Prova Resolvida Sejus ES 2013 – Vunesp). A média aritmética dos salários de 4 funcionários de uma empresa é R$ 2.500,00. A média aritmética dos salários dos dois primeiros é R$ 3.000,00, o quarto ganha R$ 500,00 a mais que o terceiro. Nesse caso, o salário do quarto empregado é igual a
(A) R$ 2.350,00.
(B) R$ 2.750,00.
(C) R$ 2.520,00.
(D) R$ 2.250,00.
(E) R$ 3.250,00.
Resolução:
Vamos chamar de x, y, z, w o salário de cada funcionários.
Como a média dos salários dos 4 é 2500:
(x + y + z + w)/4 = 2500
x + y + z + w = 4.2500
x + y + z + w = 10000 (1)
Como a média dos salários dos dois primeiros é 3000:
(x + y)/2 = 3000
x + y = 2.3000
x + y = 6000 (2)
Como o quarto ganha 500 a mais que o terceiro:
w – z = 500 (3)
Fazendo (1) – (2):
z + w = 4000 (4)
Fazendo (3) + (4):
2w = 4500
w = 4500/2 = 2250
Resposta: D
Questão 6 (Prova Resolvida PM SP 2012). João tem 5 filhos, sendo que dois deles são gêmeos. A média das idades deles é 8,6 anos. Porém, se não forem contadas as idades dos gêmeos, a média dos demais passa a ser de 9 anos. Pode-se concluir que a idade dos gêmeos, em anos, é
(A) 6,5.
(B) 7,0.
(C) 7,5.
(D) 8,0.
(E) 8,5.
Resolução:
Seja x a idade de cada um dos gêmeos.
Como a média das idades dos 3 filhos que não são gêmeos é 9, a soma das idades dos 3 é 27 anos.
Sabendo que a média dos 5 filhos é 8,6 temos:
(27 + 2x)/5 = 8,6
27 + 2x = 8,6.5
2x = 43 – 27
2x = 16
x = 16/2
x = 8 anos
Resposta: D
Clique aqui para assistir a resolução no YouTube.
Questão 7 (Prova Resolvida RFB 2009 – Esaf). Considere a seguinte amostra aleatória das idades em anos completos dos alunos em um curso preparatório. Com relação a essa amostra, marque a única opção correta:
29, 27, 25, 39, 29, 27, 41, 31, 25, 33, 27, 25, 25, 23, 27, 27, 32, 26, 24, 36, 32, 26, 28, 24, 28, 27, 24, 26, 30, 26, 35, 26, 28, 34, 29, 23, 28.
a) A média e a mediana das idades são iguais a 27.
b) A moda e a média das idades são iguais a 27.
c) A mediana das idades é 27 e a média é 26,08.
d) A média das idades é 27 e o desvio-padrão é 1,074.
e) A moda e a mediana das idades são iguais a 27.
Resolução:
Primeiramente vamos colocar as 37 idades em ordem crescente:
23, 23, 24, 24, 24, 25, 25, 25, 25, 26, 26, 26, 26, 26, 27, 27, 27, 27, 27, 27, 28, 28, 28, 28, 29, 29, 29, 30, 31, 32, 32, 33, 34, 35, 36, 39, 41.
A moda é o valor que aparece com mais frequência. Note que o 27 aparece 6 vezes e nenhum outro aparece com tanta frequência.
A mediana é o valor que, após ordenar todos os valores, se encontra no centro. Note que o 27 se encontra na posição 19º, ou seja, exatamente no meio.
Resposta: E
Questão 8 (Prova Resolvida PRF 2008 – Cespe). Ficou pior para quem bebe. O governo ainda espera a consolidação dos dados do primeiro mês de aplicação da Lei Seca para avaliar seu impacto sobre a cassação de CNHs. As primeiras projeções indicam, porém, que as apreensões subirão, no mínimo, 10%.
Antes da vigência da Lei Seca, eram suspensas ou cassadas, em média, aproximadamente 155.000 CNHs por ano. Se as previsões estiverem corretas, a média anual deve subir para próximo de 170.000. A tabela a seguir mostra esses resultados nos últimos anos( fonte: DENATRAN ).
Para que a média de CNHs suspensas ou cassadas, de 2003 a 2008, atinja o valor previsto de 170.000, será necessário que, em 2008, a quantidade de CNHs suspensas ou cassadas seja um número
A) inferior a 180.000.
B) superior a 180.000 e inferior a 200.000.
C) superior a 200.000 e inferior a 220.000.
D) superior a 220.000 e inferior a 240.000.
E) superior a 240.000
Resolução:
Para fazer a média dos 6 anos, devemos observar que em 2008 temos dados até junho. Vamos chamar de x o número de CNH cassadas ou suspensas de julho a dezembro e calcular a média:
(853900 + x) / 6 = 170000
853900 + x = 6.170000
853900 + x = 1020000
x = 1020000 – 853900 = 166100
Logo, 166100 + 64500 = 230600
Resposta: D
Questão 9 (Prova Resolvida Caixa 2006 – Cespe). A CAIXA criou as Cestas de Serviços com o compromisso de valorizar o relacionamento com seus clientes e oferecer cada vez mais vantagens.
Você paga apenas uma tarifa mensal e tem acesso aos produtos e serviços bancários que mais se adequarem ao seu relacionamento com a CAIXA.
Alguns dos itens disponíveis têm seu uso limitado. Caso você exceda as quantidades especificadas ou utilize um item não incluso na sua cesta, será cobrado o valor daquele 10 produto ou serviço discriminado na Tabela de Tarifas vigente.
A janela do PowerPoint 2003 a seguir apresenta, no slide em edição, outras informações acerca das Cestas de Serviços da CAIXA.
Com base nas informações do texto e sabendo que, a cada R$ 100,00 de saldo médio no trimestre em aplicação na poupança, o cliente acumula 1 ponto para o cálculo do desconto na tarifa mensal de serviços, julgue os seguintes itens.
Considere a seguinte situação hipotética.
Carlos, cliente da CAIXA, obteve exatamente 5 pontos relativos ao saldo médio de suas aplicações em poupança no primeiro trimestre de 2006.
Julgue a seguinte afirmação:
“Nessa situação, para dobrar essa pontuação no trimestre seguinte, caso não faça retiradas ao longo desse período, é necessário que Carlos deposite a quantia de R$ 500,00 em sua conta poupança no início de cada mês do segundo trimestre.”
ERRADO
Para que Carlos dobre sua pontuação, ele deve possuir R$ 1.000,00 de saldo médio. Note que os R$ 500,00 não serão retirados, logo as aplicações futuras devem gerar mais R$ 500,00 de saldo médio.
Pelo questão ele deve depositar R$ 500,00 durante 3 meses. Veja:
Mês 1 = Saldo 500
Mês 2 = Saldo 1000
Mês 3 = Saldo 1500
Média = 1000, que somados aos 500 que ele já tinha, são 1500.