Estudando matemática para concursos? Veja aqui tudo sobre as posições relativas entre reta e circunferência.
Não deixe de ver também nossos conteúdos sobre os outros tópicos da geometria analítica.
Bom estudo!
Seja uma circunferência λ de centro C(xc, yc) e raio r. No mesmo plano existem retas que cortam a circunferência em dois pontos, retas que tocam a circunferência em apenas um, e retas que não interceptam a circunferência. Essas retas são chamadas de secantes, tangentes e externas, respectivamente.
Veja na figura que:
A reta r (azul) é secante à circunferência, pois possuem dois pontos em comum.
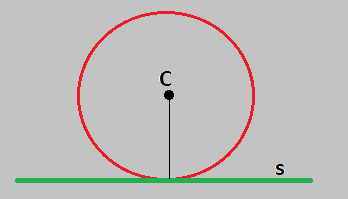
A reta s (verde) é tangente à circunferência, pois possuem apenas um ponto em comum.
A reta t (laranja) é externa à circunferência, pois não possuem nenhum ponto em comum.
RETA SECANTE
Como vimos, uma reta é secante a uma circunferência quanto possuem dois pontos em comum. A grosso modo, podemos dizer que a reta passa “por dentro” da circunferência.
Em nosso desenho, temos que a reta r é a reta secante. Nele podemos observar que a distância da reta r ao centro C da circunferência é menor que a medida do raio.
dC,r < raio
RETA TANGENTE
Definimos uma reta tangente a uma circunferência quando possuem apenas um ponto em comum.
Em nosso desenho, temos que a reta s é tangente. Nele podemos observar que a distância da reta s ao centro C da circunferência é igual à medida do raio.
dC,s = raio
RETA EXTERNA
Definimos uma reta externa a uma circunferência quando não possuem nenhum ponto em comum. A grosso modo, dizemos que a reta passa “por fora” da circunferência.
Em nosso desenho, temos que a reta t é a reta externa. Nele observamos que a distância da reta t ao centro C da circunferência é maior que a medida do raio.
dC,s > raio
COMO DETERMINAR A POSIÇÃO RELATIVA ENTRE RETA E CIRCUNFERÊNCIA
Apresentaremos agora duas formas práticas para determinarmos a posição relativa entre uma reta e uma circunferência. Para tanto, examinaremos as relações entre a reta r: 2x + y – 1 = 0 e a circunferência λ: (x + 3)² + (y – 4)² = 25.
Temos que:
2x + y – 1 = 0 é a equação geral da reta r, onde a=2, b=1 e c=-1.
(x + 3)² + (y – 4)² = 25 é a equação geral da circunferência, cujo centro é (-3, 4) e o raio é 5.
MÉTODO DA RESOLUÇÃO DO SISTEMA DE EQUAÇÕES
Por este método, a resolução dá-se resolvendo o sistema de duas variáveis, x e y, e duas equações, da reta e da circunferência.
Nosso objetivo será resolver o seguinte sistema:
2x + y – 1 = 0
(x + 3)² + (y – 4)² = 25
Isolando a variável y na equação 1:
y = 1 – 2x
Substituindo na equação 2:
(x + 3)² + (y – 4)² = 25
(x + 3)² + (1 – 2x – 4)² = 25
x² + 6x + 9 + (-2x – 3)² – 25 = 0
x² + 6x + 9 + 4x² + 12x + 9 – 25 = 0
5x² + 18x – 7 = 0
Δ = b² – 4.a.c
Δ = 18² – 4.5.(-7)
Δ = 324 + 140
Δ = 464
Como Δ > 0, a equação do segundo grau 5x² + 18x – 7 = 0 possui duas raízes. Podemos concluir que existem dois pontos em comum e que a reta r é secante a circunferência λ.
MÉTODO DO CÁLCULO DA DISTÂNCIA
Por este método, calculamos a distância da reta ao centro da circunferência e a comparamos com a medida do raio.
Nosso primeiro objetivo será calcular a distância, que pode ser feito através da seguinte fórmula:
Onde:
(x0, y0) é o centro da circunferência.
ax + by + c = 0 é a equação geral da reta.
Como o raio da circunferência é igual a 5, e a distância entre a reta e a circunferência é igual a 1,3, podemos concluir que a reta é secante a circunferência.
Gostou da nossa página sobre as posições relativas entre reta e circunferência?
Deixe o seu comentário.