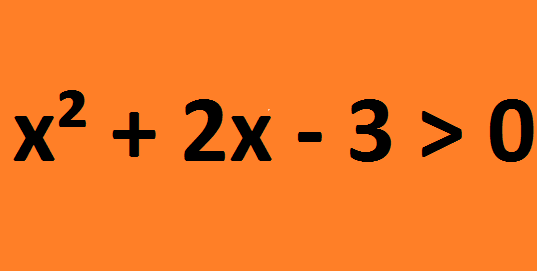Nesta página vamos aprender a resolver inequações do segundo grau. O ideal é que você já tenha estudado sobre equações e funções do segundo grau.
Por mais que o assunto gere muitas dúvidas, você verá como é simples quando analisamos através da parábola associada.
Bom estudo!
Introdução
Diferente das equações do segundo grau, onde temos igualdades, nas inequações do segundo grau nós utilizamos outros símbolos. São eles:
> (maior)
< (menor)
≥ (maior ou igual)
≤ (menor ou igual)
Como Resolver
Resolver uma inequação do segundo grau nada mais é do que estudar o sinal da função quadrática associada a inequação. Veja como funciona:
Dada a inequação do segundo grau do tipo ax² + bx + c > 0.
A função do segundo grau a ela associada é f(x) = ax² + bx + c.
Devemos então analisar quando temos f(x) > 0.
E como podemos saber quando a função f é maior que zero? A resposta é simples, analisando o gráfico de f(x). Quem já estudou o conteúdo sobre funções do segundo grau já sabe que o gráfico desse tipo de função é uma parábola.
Vamos Praticar?
Agora que já aprendemos na teoria como resolver inequações do segundo grau, vamos praticar com alguns exemplos para fixarmos melhor o conteúdo, afinal é praticando que se aprende, não é mesmo?
Exemplo 1:
Resolver a inequação x² – 3x ≤ 0.
Como vimos, devemos associar essa inequação a uma função do segundo grau.
f(x) = x² – 3x
Onde queremos saber quando f(x) ≤ 0.
Analisando a função f, temos que a=1, b=-3 e c=0, daí já sabemos que o gráfico é uma parábola com a concavidade para cima, pois a>0.
Outra informação importante que precisamos para analisarmos o sinal de f são as raízes dessa função.
Resolvendo a equação do segundo grau:
x² – 3x = 0
x(x – 3) = 0
Temos que x=0 ou x=-3.
Daí, as raízes de f são -3 e 0.
Pronto. Já sabemos se a parábola é voltada para cima ou para baixo e as raízes da função. Agora já podemos resolver a inequação.
Veja o gráfico da função f com as informações que temos:
E agora, quando é que f(x) ≤ 0???????
Nota-se que isto acontece quando x está entre 0 e 3, incluindo-se esses dois números. Temos então um intervalo real que pode ser representado como [0, 3].
Daí, podemos representar o conjunto solução da inequação x² – 3x ≤ 0 de duas formas:
S = [0, 3]
ou
S = {x∈R | 0 ≤ x ≤ 3}.
Exemplo 2.
x² + 3x + 7 > 10 + x
Veja que a inequação do exemplo não está “organizada”. Precisamos modificá-la, de modo que consigamos identificar os valores de a, b e c.
x² + 3x + 7 > 10 + x
x² + 3x + 7 – 10 – x > 0
x² + 2x – 3 > 0
Precisamos agora analisar os sinais da função quadrática f(x) = x² + 2x – 3, onde sabemos que a=1, b=3 e c=-3.
A primeira informação que podemos tirar é que a parábola da função f possui a concavidade para cima, pois a>0.
Vamos agora descobrir as raízes da função, e vamos fazer isso utilizando a fórmula de Bhaskara:
Calculando o valor de Δ:
Δ = b² – 4ac
Δ = 2² – 4.1.(-3)
Δ = 4 + 12
Δ = 16
Calculando as raízes:
Daí, as raízes da função f são -3 e 1.
Agora que já sabemos o sentido da parábola e as raízes da função, podemos representar o gráfico de f:
E agora, quando é que f(x) > 0???????
Nota-se que isto acontece quando x é menor que -3, ou quando x é maior que 1. Temos então dois intervalos reais que podem ser representados como ]∞, -3[ e ]1, ∞[
Daí, podemos representar o conjunto solução da inequação x² + 2x – 3 > 0 de duas formas:
S = ]∞, -3[ + ]1, ∞[
ou
S = {x∈R | x<-3 ou x>1}.
Aprendeu a resolver inequações do segundo grau? Como pode perceber, é muito importante que o estudante já domine os conteúdos e equação e função do segundo grau.
Se gostou, compartilhe nas redes sociais e deixe seu comentário. Se não gostou, mande também seu comentário pra gente para que possamos melhorar cada vez mais nessa nossa busca pela melhoria do ensino da matemática.
Boa sorte a todos e fiquem com Deus!