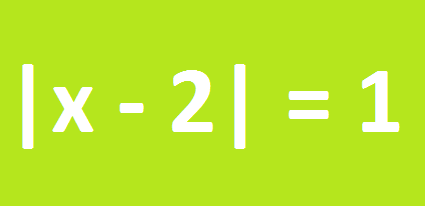Relacionamos nesta página alguns exercícios resolvidos sobre o módulo ou valor absoluto de um número real.
A matéria não é complicada, apenas exige um pouco de atenção dos estudantes.
Bons estudos!
1. Calcule, usando a definição de módulo:
a) |-13| = 13
b) |50| = 50
c) |0| = 0
d) |-1| = 1
e) |-π| = π
f) |-√3| = √3
g) |√3| = √3
2. Ache os valores de:
a) |-3 + 4| = |1| = 1
b) |5 – 16| = |-11| = 11
c) |1,3 – 4,5| = |-3,2| = 3,2
d) |√3 – 1| = √3 – 1
e) |2 – π| = π – 2
f) |1 – √3| = √3 – 1
3. Qual é o valor de y = |√2 – 1| – |1 – √2|?
Vamos resolver por partes:
|√2 – 1| = √2 – 1
|1 – √2| = √2 – 1
Daí,
√2 – 1 – (√2 – 1) = 0
4. Simplifique a fração abaixo:
Pela definição de módulo, temos que:
|x – 2| = x – 2, se x ≥ 2
|x – 2| = -(x – 2), se x < 2
Para resolver o exercício temos dois casos a considerar:
Se x ≥ 2
Se x < 0