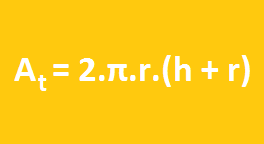Procurando exercícios resolvidos sobre o cálculo da área de um cilindro? Confira aqui várias questões resolvidas, todas retiradas das últimas provas de concursos.
Não deixe de ver também nossos exercícios resolvidos sobre outros conteúdos da geometria espacial.
Bom estudo!
Questão 1 (Liquigás – Cesgranrio 2012). Um cilindro circular reto possui altura igual ao raio de sua base. Se a razão entre o volume do cilindro, dado em metros cúbicos, e a sua área total, dada em metros quadrados, é igual a 2 metros, então a área lateral do cilindro, em m² , é igual a
a) 128π
b) 64π
c) 48π
d) 32π
e) 16π
Resolução
A questão informa que a altura e o raio do cilindro possuem a mesma medida. Vamos considerar que h = r = x. Temos:
Volume do cilindro:
V = π.r².h = π.x².x = π.x³
Área total do cilindro:
A = 2.π.r(h + r) = 2.π.x(x + x) = 2.π.x(2x) = 4.π.x²
Como a razão V/A = 2, temos:
Assim, a altura e o raio do cilindro medem 8 metros.
Calculando a área lateral:
Al = 2.π.r.h
Al = 2.π.8.8
Al = 128π
Resposta: A
Questão 2 (Petrobras – Cesgranrio 2012). Uma fita retangular de 2 cm de largura foi colocada em torno de uma pequena lata cilíndrica de 12 cm de altura e 192π cm³ de volume, dando uma volta completa em torno da lata, como ilustra o modelo abaixo.
A área da região da superfície da lata ocupada pela fita é, em cm² , igual a
a) 8π
b) 12π
c) 16π
d) 24π
e) 32π
Resolução
A informação que ainda não temos para calcular a área pedida é o raio da base do cilindro.
Nosso objetivo inicial será utilizar a medida da altura e do volume para descobrirmos o raio.
Utilizando a fórmula do volume:
V = π.r².h
192π = π.r².12
192 = 12r²
r² = 192/12
r² = 16
r = 4 cm
Agora que sabemos a medida do raio, vamos calcular a área lateral ocupada pela fita, cuja altura é de 2 cm.
Al = 2.π.r.h
Al = 2.π.4.2
Al = 16.π cm²
Resposta: C